题目内容
(08年沈阳二中四模)(12分)
在棱长为![]() 的斜三棱柱
的斜三棱柱![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() ,连结
,连结![]() 。
。
(Ⅰ)求证:![]() ⊥平面
⊥平面![]() ;
;
(Ⅱ)求二面角![]() 的大小。
的大小。
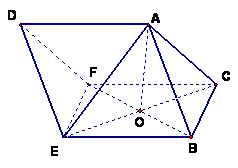
解析:(Ⅰ)![]() 证明:∵
证明:∵![]() 是菱形,
是菱形,
∴ ![]() ⊥
⊥![]()
又∵ ![]() ⊥
⊥![]() ,且
,且![]()
∴![]() ⊥平面
⊥平面![]() , ……………3分
, ……………3分
而AO![]() 平面
平面![]()
∴![]() ⊥
⊥![]()
∵![]() ,
,![]() ∴
∴![]()
∴![]() ⊥
⊥![]() ,且
,且![]()
∴![]() ⊥平面
⊥平面![]() .…………6分
.…………6分
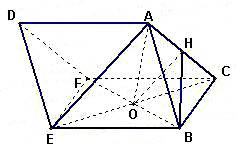
(Ⅱ) 取![]() 的中点
的中点![]() ,连结
,连结![]() 、
、![]()
∵![]() 是等边三角形 ∴
是等边三角形 ∴![]() ⊥
⊥![]()
∵![]() ⊥平面
⊥平面![]() ∴
∴![]() 是
是![]() 在平面
在平面
![]() 上的射影,
上的射影,
∴由三垂线定理逆定理 可得![]()
∴![]() 是二面角
是二面角![]() 的平面角………………………………………………9分
的平面角………………………………………………9分
![]() ≌Rt
≌Rt![]() ,则
,则![]() ,∴四边形
,∴四边形![]() 为正方形。
为正方形。
在直角三角形![]() 中,
中,![]() ,
,![]() ∴
∴![]() =
=![]() =
=![]()
∴![]() =arcsin
=arcsin![]() .(或
.(或![]() ,
,![]() )
)
∴二面角![]() 的大小是arcsin
的大小是arcsin![]() …………………………………………12分
…………………………………………12分

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目

