摘要：3．利用向量处理角度问题 在立体几何中.涉及的角有异面直线所成的角.直线与平面所成的角.二面角等.关于角的计算.均可归结为两个向量的夹角.对于空间向量.有.利用这一结论.我们可以较方便地处理立体几何中的角的问题. 求异面直线所成的角的关键在于求异面直线上两向量的数量积.而要求两向量的数量积.可以求两向量的坐标.也可以把所求向量用一组基向量表示.两向量的夹角范围是.而两异面直线所成角的范围是.应注意加以区分. 直线与平面的夹角.是直线的方向向量与平面的法向量的夹角的余角.故有:.. 设分别是二面角的面的法向量.则＜＞就是所求二面角的平面角或其补角的大小.
网址：http://m.1010jiajiao.com/timu_id_4327483[举报]
（2009全国卷Ⅱ文）（本小题满分12分）
|
|
（Ⅰ）求a,b的值；
（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有
成立？
若存在，求出所有的P的坐标与l的方程；若不存在，说明理由。
解析：本题考查解析几何与平面向量知识综合运用能力，第一问直接运用点到直线的距离公式以及椭圆有关关系式计算，第二问利用向量坐标关系及方程的思想，借助根与系数关系解决问题，注意特殊情况的处理。
查看习题详情和答案>>（2009全国卷Ⅱ文）（本小题满分12分）
|
|
（Ⅰ）求a,b的值；
（Ⅱ）C上是否存在点P，使得当l绕F转到某一位置时，有
成立？
若存在，求出所有的P的坐标与l的方程；若不存在，说明理由。
解析：本题考查解析几何与平面向量知识综合运用能力，第一问直接运用点到直线的距离公式以及椭圆有关关系式计算，第二问利用向量坐标关系及方程的思想，借助根与系数关系解决问题，注意特殊情况的处理。
查看习题详情和答案>>
如图，四边形ABCD是矩形，PA⊥平面ABCD，AP=AB=2，BC=2| 2 |
（Ⅰ）证明：PC⊥平面BEF；
（Ⅱ）求平面BEF与平面BAP夹角的大小．
（理科做）如图所示已知在矩形ABCD中，AB=1，BC=a（a＞0），PA⊥平面ABCD且PA=1．建立适当的空间坐标系，利用空间向量求解下列问题：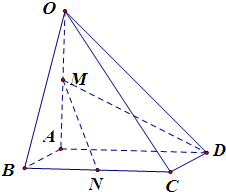
如图，在四棱锥O-ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA=2，M为OA的中点，N为BC中点，以A为原点，建立适当的空间直角坐标系，利用空间向量解答以下问题