摘要： 证明四边形的四条边相等 例1 已知:如图1.C是线段BD上一点.和都是等边三角形.R.F.G.H分别是四边形ABDE各边的中点.求证:四边形RFGH是菱形. 证明:连结AD.BE 因为和都是等边三角形 所以 故四边形RFGH是菱形
网址：http://m.1010jiajiao.com/timu_id_4056305[举报]
已知：如图，四边形ABCD是平行四边形，F、G是AB边上的两个点，且FC平分∠BCD，G
D平分∠ADC，FC与GD相交于点E．
（1）求证：AF=GB；
（2）请将平行四边形ABCD添加一个什么条件，使得△EFG为等腰直角三角形，并说明理由． 查看习题详情和答案>>
D平分∠ADC，FC与GD相交于点E．（1）求证：AF=GB；
（2）请将平行四边形ABCD添加一个什么条件，使得△EFG为等腰直角三角形，并说明理由． 查看习题详情和答案>>
已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF．请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和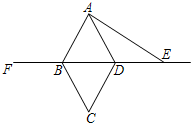
图中已有的某一条线段相等（只须证明一组线段相等即可）．
（1）连接 ；
（2）猜想： = ；
（3）证明：（说明：写出证明过程的重要依据） 查看习题详情和答案>>
图中已有的某一条线段相等（只须证明一组线段相等即可）．（1）连接
（2）猜想：
（3）证明：（说明：写出证明过程的重要依据） 查看习题详情和答案>>
已知：如图，抛物线c1经过A，B，C三点，顶点为D，且与x轴的另一个交点为E．
（1）求抛物线c1解析式；
（2）求四边形ABDE的面积；
（3）△AOB与△BDE是否相似，如果相似，请予以证明；如果不相似，请说明理由；
（4）设抛物线c1的对称轴与x轴交于点F，另一条抛物线c2经过点E（抛物线c2与抛物线c1不重合），且顶点为M（a，b），对称轴与x轴相交于点G，且以M，G，E为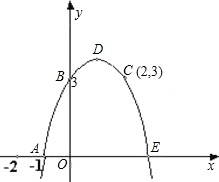
顶点的三角形与以D，E，F为顶点的三角形全等，求a，b的值．（只需写出结果，不必写出解答过程）
查看习题详情和答案>>
（1）求抛物线c1解析式；
（2）求四边形ABDE的面积；
（3）△AOB与△BDE是否相似，如果相似，请予以证明；如果不相似，请说明理由；
（4）设抛物线c1的对称轴与x轴交于点F，另一条抛物线c2经过点E（抛物线c2与抛物线c1不重合），且顶点为M（a，b），对称轴与x轴相交于点G，且以M，G，E为
顶点的三角形与以D，E，F为顶点的三角形全等，求a，b的值．（只需写出结果，不必写出解答过程）
查看习题详情和答案>>
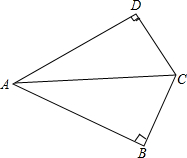已知：如图，四边形ABCD中，AC平分∠BAD，∠B和∠D都是直角．
已知：如图，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE=BF．请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）．