摘要： 已知1<m<n.m.n∈N*.求证:(1+m)n>(1+n)m. 证法一:由二项式定理(1+m)n=Cm0+Cm1+-+Cmn. (1+n)m=Cn0+Cn1+-+C. 又因为C=.C=. 而Ami>A.所以Cm2>C.C>Cn3.-.C>C. 又因为C=C.C=C. 所以(1+m)n>(1+n)m. 证法二:(1+m)n>(1+n)mnln(1+m)>mln(1+n) >. 令f(x)=.x∈［2.+∞］. 只要证f(x)在［2.+∞］上单调递减.只要证f ′(x)<0. f ′(x)==. 当x≥2时.x-lg(1+x)<0. x2(1+x)>0.得f ′(x)<0.即x∈［2,+∞］时.f ′(x)<0. 以上各步都可逆推.得(1+m)n>(1+n)m. [探索题]已知数列是首项是a1.公比为q的等比数列. (1)求和: 的结果归纳概括出关于正整数n的一个结论.并加以证明. (3)设q≠1.Sn是等比数列的前n项和.求: . 解:(1) (2)归纳概括的结论为: 若数列是首项为a1.公比为q的等比数列.则 (3)因为
网址：http://m.1010jiajiao.com/timu_id_4052214[举报]
B、
D、m，n的关系不能确定（08年南昌市一模理）（12分）已知函数f (x) =lnx,g(x) =
，（a为常数），若直线l与y =f(x), y =g(x)的图象都相切，且l与y = f(x)的图象相切的切点的横坐标为1.
（1）求直线l的方程及a的值；
（2） 当 2 ≤m <
时,求h(x)= f(x)―f
(x)[2g(x)- m +1]在[
,2]上的最大值.
（09年临沂一模理）（12分）
已知点M在椭圆
（a>b>0）上，以M为圆心的圆与x轴相切于椭圆的右焦点F。
(1)若圆M与y轴相交于A、B两点，且△ABM是边长为2的正三角形，求椭圆的方程;
(2)若点F（1,0），设过点F的直线l交椭圆于C、D两点，若直线l绕点F任意转动时恒有|OC|2+|OD|2<|CD|2，求a的取值范围。
查看习题详情和答案>>
,A的一个特征值
，其对应的特征向量是
.
；
在矩阵M所对应的线性变换下的像的方程
．以极点为平面直角坐标系的原点，极轴为x轴的正半轴，建立平面直角坐标系，直线l的参数方程是：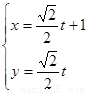
，求直线l与曲线C相交所成的弦的弦长．
R，对任意的a∈（-l，1），总存在xo∈[1，e]，使得不等式ma － (xo)<0成立，求实数m的取值范围；
∈N*）．