摘要:2.空间向量的运算 定义:与平面向量运算一样.空间向量的加法.减法与数乘向量运算如下 运算律:⑴加法交换律: ⑵加法结合律: ⑶数乘分配律: 3 共线向量 表示空间向量的有向线段所在的直线互相平行或重合.则这些向量叫做共线向量或平行向量.平行于记作. 当我们说向量.共线(或//)时.表示.的有向线段所在的直线可能是同一直线.也可能是平行直线.
网址:http://m.1010jiajiao.com/timu_id_4051528[举报]
如图,已知向量![]() ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若![]()
![]() ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算![]() ,显然
,显然![]() 的结果仍为一向量,记作
的结果仍为一向量,记作![]() .
.

求证:向量![]() 为平面
为平面![]() 的法向量;
的法向量;
求证:以![]() 为边的平行四边形
为边的平行四边形![]() 的面积等于
的面积等于![]() ;
;
将四边形![]() 按向量
按向量![]() 平移,得到一个平行六面体
平移,得到一个平行六面体![]() ,试判断平行六面体的体积
,试判断平行六面体的体积![]() 与
与![]() 的大小.
的大小.
如图,已知向量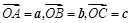 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若
 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算 ,显然
,显然 的结果仍为一向量,记作
的结果仍为一向量,记作 .
.
1、求证:向量 为平面
为平面 的法向量;
的法向量;
2、求证:以 为边的平行四边形
为边的平行四边形 的面积等于
的面积等于 ;
;
将四边形 按向量
按向量 平移,得到一个平行六面体
平移,得到一个平行六面体 ,试判断平行六面体的体积
,试判断平行六面体的体积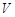 与
与 的大小.
的大小.

查看习题详情和答案>>
如图,已知向量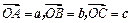 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若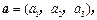
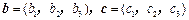 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算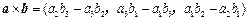 ,显然
,显然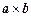 的结果仍为一向量,记作
的结果仍为一向量,记作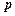 .
.
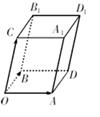
(1) 求证:向量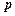 为平面
为平面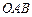 的法向量;
的法向量;
(2) 求证:以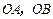 为边的平行四边形
为边的平行四边形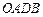 的面积等于
的面积等于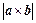 ;
;
(3) 将四边形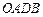 按向量
按向量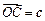 平移,得到一个平行六面体
平移,得到一个平行六面体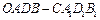 ,试判断平行六面体的体积
,试判断平行六面体的体积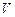 与
与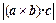 的大小.
的大小.
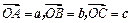 ,可构成空间向量的一个基底,若
,可构成空间向量的一个基底,若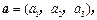
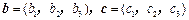 ,在向量已有的运算法则的基础上,新定义一种运算
,在向量已有的运算法则的基础上,新定义一种运算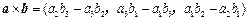 ,显然
,显然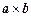 的结果仍为一向量,记作
的结果仍为一向量,记作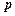 .
.
(1) 求证:向量
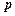 为平面
为平面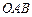 的法向量;
的法向量;(2) 求证:以
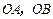 为边的平行四边形
为边的平行四边形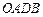 的面积等于
的面积等于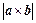 ;
;(3) 将四边形
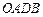 按向量
按向量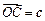 平移,得到一个平行六面体
平移,得到一个平行六面体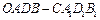 ,试判断平行六面体的体积
,试判断平行六面体的体积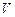 与
与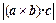 的大小.
的大小.
