摘要:三棱锥被平行于底面ABC的平面所截得的几何体如图所示.截面为A1B1C1. ∠BAC=90°,A1A⊥平面ABC,A1A=,AB=,AC=2,A1C1=1,=. (1)证明:平面A1AD⊥平面BCC1B1, (2)求二面角A-CC1-B的余弦值. 方法一 (1)证明 ∵A1A⊥平面ABC,BC平面ABC, ∴A1A⊥BC. 在Rt△ABC中,AB=,AC=2,∴BC=. ∵BD∶DC=1∶2,∴BD=.又==, ∴△DBA∽△ABC,∴∠ADB=∠BAC=90°, 即AD⊥BC. 又A1A∩AD=A,∴BC⊥平面A1AD. ∵BC平面BCC1B1,∴平面A1AD⊥平面BCC1B1. (2)解 如图①,作AE⊥C1C交C1C于E点,连接BE,由已知得AB⊥平面ACC1A1, ∴AE是BE在平面ACC1A1内的射影. 由三垂线定理知BE⊥CC1, ∴∠AEB为二面角A-CC1-B的平面角. 图① 过C1作C1F⊥AC交AC于F点, 则CF=AC-AF=1, C1F=A1A=,∴∠C1CF=60°. 在Rt△AEC中, AE=ACsin60°=2×=, 在Rt△BAE中,tan∠AEB===, ∴cos∠AEB=, 即二面角A-CC1-B余弦值为. 方法二 (1) 证明 如图②,建立空间直角坐标系, 图② 则A,B(,0,0),C, A1(0,0,),C1(0,1, ). ∵BD∶DC=1∶2,∴=, ∴D点坐标为, ∴=, =(-,2,0),=(0,0,). ∵·=0.·=0. ∴BC⊥AA1.BC⊥AD.又A1A∩AD=A. ∴BC⊥平面A1AD.又BC平面BCC1B1. ∴平面A1AD⊥平面BCC1B1. (2)解 ∵BA⊥平面ACC1A1.取m==(,0,0)为平面ACC1A1的法向量. 设平面BCC1B1的法向量为n=, 则·n=0.·n=0. ∴ ∴x=y.z=.可取y=1.则n=. cos〈m,n〉= =, 即二面角A-CC1-B的余弦值为.
网址:http://m.1010jiajiao.com/timu_id_4039546[举报]
 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=| 3 |
| 2 |
| BD |
| DC |
| 1 |
| 2 |
(Ⅰ)证明:平面A1AD⊥平面BCC1B1;
(Ⅱ)求二面角A-CC1-B的大小. 查看习题详情和答案>>
 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,A1A=| 3 |
| 2 |
| BD |
| DC |
| 1 |
| 2 |
(Ⅰ)证明:平面A1AD⊥平面BCC1B1;
(Ⅱ)求AA1与平面BCC1B1所成角的正弦值. 查看习题详情和答案>>
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,
∠BAC=90°,A1A⊥平面ABC,A1A=![]() ,AB=
,AB=![]() ,AC=2,A1C1=1,
,AC=2,A1C1=1,![]() =
=![]() .
.
(1)证明:平面A1AD⊥平面BCC1B1;
(2)求二面角A—CC1—B的余弦值.

 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC, ,
,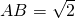 ,AC=2,A1C1=1,
,AC=2,A1C1=1, .
. 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,∠BAC=90°,A1A⊥平面ABC,