摘要:在平面直角坐标系xOy中.已知点A.B, 动点C满足 条件:△ABC的周长为2+2.记动点C的轨迹为曲线W. (Ⅰ) 求W的方程, 且斜率为k的直线l与曲线W 有两个不同的交点P和Q.求k 的取值范围, (Ⅲ)已知点M(.0).N的条件下.是否存在常数k.使得向量 与共线?如果存在.求出k的值,如果不存在.请说明理由.
网址:http://m.1010jiajiao.com/timu_id_4038412[举报]
(本小题满分15分)平面直角坐标系xOy中,已知⊙M经过点F1(0,-c),F2(0,c),A( c,0)三点,其中c>0.
c,0)三点,其中c>0.
(1)求⊙M的标准方程(用含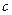 的式子表示);
的式子表示);
(2)已知椭圆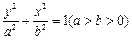 (其中
(其中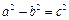 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,
⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
 c,0)三点,其中c>0.
c,0)三点,其中c>0.(1)求⊙M的标准方程(用含
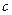 的式子表示);
的式子表示);(2)已知椭圆
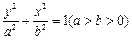 (其中
(其中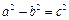 )的左、右顶点分别为D、B,
)的左、右顶点分别为D、B,⊙M与x轴的两个交点分别为A、C,且A点在B点右侧,C点在D点右侧.
①求椭圆离心率的取值范围;
②若A、B、M、O、C、D(O为坐标原点)依次均匀分布在x轴上,问直线MF1与直线DF2的交点是否在一条定直线上?若是,请求出这条定直线的方程;若不是,请说明理由.
(本小题满分15分)
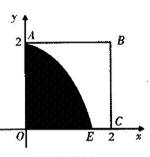
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.

(1)当 时,求直路
时,求直路 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
查看习题详情和答案>>
(本小题满分15分)
在平面直角坐标系中,已知点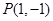 ,过点
,过点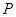 作抛物线
作抛物线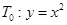 的切线,其切点分别为
的切线,其切点分别为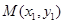 、
、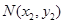 (其中
(其中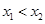 ).
).
(1)求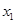 与
与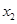 的值;
的值;
(2)若以点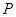 为圆心的圆
为圆心的圆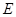 与直线
与直线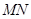 相切,求圆
相切,求圆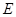 的面积;
的面积;
(3)过原点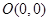 作圆
作圆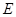 的两条互相垂直的弦
的两条互相垂直的弦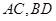 ,求四边形
,求四边形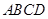 面积的最大值.
面积的最大值.
查看习题详情和答案>>
 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数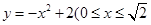 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为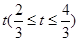 .
.
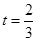 时,求直路
时,求直路 系中,已知点
系中,已知点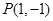 ,过点
,过点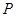 作抛物线
作抛物线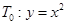 的切线,其切点分别为
的切线,其切点分别为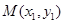 、
、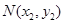 (其中
(其中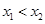 ).
).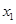 与
与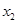 的值;
的值;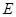 与直线
与直线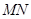 相切,求圆
相切,求圆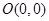 作圆
作圆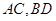 ,求四边形
,求四边形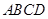 面积的最大值.
面积的最大值.