题目内容
(本小题满分15分)
如图,某小区有一边长为2(单位:百米)的正方形地块OABC,其中OAE是一个游泳池,计划在地块OABC内修一条与池边AE相切的直路 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.

(1)当 时,求直路
时,求直路 所在的直线方程;
所在的直线方程;
(2)当t为何值时,地块OABC在直路 不含泳池那侧的面积取到最大,最大值是多少?
不含泳池那侧的面积取到最大,最大值是多少?
【答案】
(1)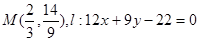 ;(2)
;(2)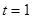 ,
,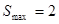 。
。
【解析】
试题分析:(1)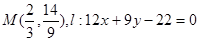
(2)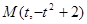 ,过切点M的切线
,过切点M的切线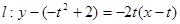
即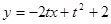 ,令
,令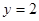 得
得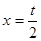 ,故切线
,故切线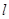 与AB交于点
与AB交于点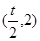 ;
;
令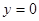 ,得
,得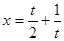 ,又
,又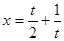 在
在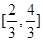 递减,所以
递减,所以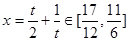
故切线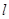 与OC交于点
与OC交于点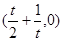 。
。
 地块OABC在切线
地块OABC在切线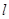 右上部分区域为直角梯形,
右上部分区域为直角梯形,
面积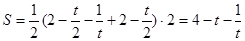
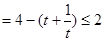 ,等号
,等号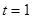 ,
,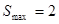 。
。
考点:本题主要考查函数模型,导数的几何意义,导数的应用,均值定理的应用。
点评:中档题,注意仔细审题。运用导数的几何意义,求切线方程属于简单题,解题的关键是建立面积的表达式后,通过构造,创造了应用均值定理的条件,“一正、二定、三相等”。

练习册系列答案
相关题目

 的单调区间;
的单调区间; ,试分别解答以下两小题.
,试分别解答以下两小题. 对任意的
对任意的 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 是两个不相等的正数,且
是两个不相等的正数,且 ,求证:
,求证: .
. 、
、 分别为椭圆
分别为椭圆 :
: 的
的  :
: 的焦点,
的焦点, 是
是 。
。 :
: ,过点P的动直线
,过点P的动直线 与圆
与圆 ,
, (
( 且
且 )。求证:点Q总在某定直线上。
)。求证:点Q总在某定直线上。
 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
 在定义域内存在区间
在定义域内存在区间 ,满足
,满足 是否为“优美函数”?若是,求出
是否为“优美函数”?若是,求出 ;若不是,说明理由;
;若不是,说明理由; 为“优美函数”,求实数
为“优美函数”,求实数 的取值范围.
的取值范围.