摘要:22. 设A.B为椭圆上的两个动点. (1)若A.B满足.其中O为坐标原点.求证:为定值, (2)若过A.B的椭圆的两条切线的交点在直线x+2y=5上.求证直线AB恒过一个定点.
网址:http://m.1010jiajiao.com/timu_id_4037619[举报]
(本小题满分14分)已知A、B、C是椭圆![]() 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为![]() ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且![]() .(1)求椭圆
.(1)求椭圆![]() 的方程;(2)过点
的方程;(2)过点![]() 的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且
的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且![]() .求实数t的取值范围.
.求实数t的取值范围.
(本小题满分14分)

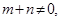 直线
直线 是线段
是线段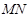 的垂直平分线.设椭圆E的方程为
的垂直平分线.设椭圆E的方程为 .
.
(1)当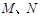 在
在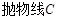 上移动时,求直线
上移动时,求直线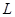 斜率
斜率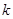 的取值范围;
的取值范围;
(2)已知直线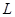 与抛物线
与抛物线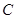 交于A、B两个不同点,
交于A、B两个不同点, 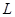 与椭圆
与椭圆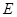 交于P、Q两个不同点,设AB中点为
交于P、Q两个不同点,设AB中点为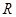 ,OP中点为
,OP中点为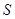 ,若
,若 ,求椭圆
,求椭圆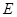 离心率的范围。
离心率的范围。
查看习题详情和答案>>
(本小题满分14分)
已知椭圆 的焦点F与抛物线C:
的焦点F与抛物线C: 的焦点关于直线x-y=0
的焦点关于直线x-y=0
对称.
(Ⅰ)求抛物线的方程;
(Ⅱ)已知定点A(a,b),B(-a,0)(ab ),M是抛物线C上的点,设直线AM,
),M是抛物线C上的点,设直线AM,
BM与抛物线的另一交点为 .求证:当M点在抛物线上变动时(只要
.求证:当M点在抛物线上变动时(只要 存在
存在
且 )直线
)直线 恒过一定点,并求出这个定点的坐标.
恒过一定点,并求出这个定点的坐标.
查看习题详情和答案>>
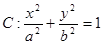
 的顶点为
的顶点为 焦点为
焦点为
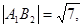 S□
S□ = 2S□
= 2S□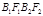 .
.
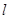 过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线
过P(1,1),且与椭圆相交于A,B两点,当P是AB的中点时,求直线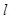 是与n垂直相交于P点、与
是与n垂直相交于P点、与 ,是否存在上述直线
,是否存在上述直线 (本小题满分14分)
(本小题满分14分)