摘要:20. 已知函数.. (1)当时.若上单调递减.求a的取值范围, (2)求满足下列条件的所有整数对:存在.使得的最大值. 的最小值, (3)对满足(II)中的条件的整数对.试构造一个定义在且 上的函数:使.且当时.. 附加题
网址:http://m.1010jiajiao.com/timu_id_4034402[举报]
(本题满分16分)已知函数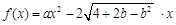 ,
,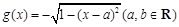 .
.
(1)当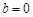 时,若
时,若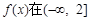 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对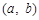 :存在
:存在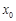 ,使得
,使得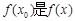 的最大值,
的最大值,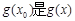 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对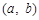 ,试构造一个定义在
,试构造一个定义在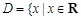 且
且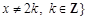 上的函数
上的函数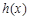 :使
:使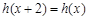 ,且当
,且当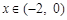 时,
时,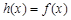 .
.
查看习题详情和答案>>
(本题满分16分)
已知函数![]() ,
,![]() .
.
(1)当![]() 时,若
时,若![]() 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对![]() :存在
:存在![]() ,使得
,使得![]() 的最大值,
的最大值,![]() 的最小值;
的最小值;
(3)对满足(II)中的条件的整数对![]() ,试构造一个定义在
,试构造一个定义在![]() 且
且![]() 上的函数
上的函数![]() :使
:使![]() ,且当
,且当![]() 时,
时,![]() .
.
(本题满分16分)已知函数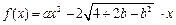 ,
,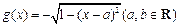 .
.
(1)当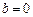 时,若
时,若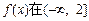 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;
(2)求满足下列条件的所有整数对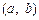 :存在
:存在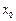 ,使得
,使得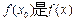 的最大值,
的最大值,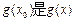 的最小值;
的最小值;
(3)对满足(2)中的条件的整数对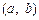 ,试构造一个定义在
,试构造一个定义在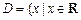 且
且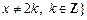 上的函数
上的函数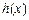 :使
:使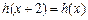 ,且当
,且当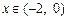 时,
时,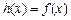 .
.
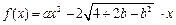 ,
,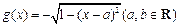 .
.(1)当
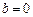 时,若
时,若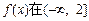 上单调递减,求a的取值范围;
上单调递减,求a的取值范围;(2)求满足下列条件的所有整数对
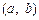 :存在
:存在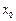 ,使得
,使得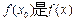 的最大值,
的最大值,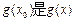 的最小值;
的最小值;(3)对满足(2)中的条件的整数对
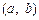 ,试构造一个定义在
,试构造一个定义在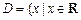 且
且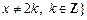 上的函数
上的函数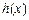 :使
:使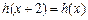 ,且当
,且当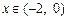 时,
时,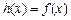 .
.