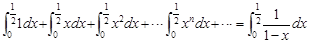摘要:1.数学思想方法的重要性 数学思想方法的教学是中学数学教学中的重要组成部分.有利于学生加深数学知识的理解和掌握. 本章重视与内容密切相关的数学思想方法的教学.并且在提出问题.思考解决问题的策略等方面对学生进行具体示范.引导.本章的两个主要数学结论是正弦定理和余弦定理.它们都是关于三角形的边角关系的结论.在初中.学生已经学习了相关边角关系的定性的知识.就是“在任意三角形中有大边对大角.小边对小角 .“如果已知两个三角形的两条对应边及其所夹的角相等,那么这两个三角形全 等. 教科书在引入正弦定理内容时.让学生从已有的几何知识出发.提出探究性问题:“在任意三角形中有大边对大角.小边对小角的边角关系.我们是否能得到这个边.角的关系准确量化的表示呢? .在引入余弦定理内容时.提出探究性问题“如果已知三角形的两条边及其所夹的角,根据三角形全等的判定方法.这个三角形是大小.形状完全确定的三角形.我们仍然从量化的角度来研究这个问题.也就是研究如何从已知的两边和它们的夹角计算出三角形的另一边和两个角的问题. 设置这些问题.都是为了加强数学思想方法的教学.
网址:http://m.1010jiajiao.com/timu_id_4033473[举报]
(2013•福建)当x∈R,|x|<1时,有如下表达式:1+x+x2+…+xn+…=
两边同时积分得:
1dx+
xdx+
x2dx+…
xndx+…=
dx
从而得到如下等式:1×
+
×(
)2+
×(
)3+…+
×(
)n+1+…=ln2.
请根据以上材料所蕴含的数学思想方法,计算:
×
+
×(
)2+
×(
)3+…+
×(
)n+1=
[(
)n+1-1]
[(
)n+1-1].
查看习题详情和答案>>
| 1 |
| 1-x |
两边同时积分得:
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| ∫ |
0 |
| 1 |
| 1-x |
从而得到如下等式:1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| n+1 |
| 1 |
| 2 |
请根据以上材料所蕴含的数学思想方法,计算:
| C | 0 n |
| 1 |
| 2 |
| 1 |
| 2 |
| C | 1 n |
| 1 |
| 2 |
| 1 |
| 3 |
| C | 2 n |
| 1 |
| 2 |
| 1 |
| n+1 |
| C | n n |
| 1 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
| 1 |
| n+1 |
| 3 |
| 2 |
已知函数![]() 的定义域为
的定义域为![]() 且
且![]() ,对任意
,对任意![]() 都有
都有![]()
![]()
数列![]() 满足
满足![]() N
N![]() .证明函数
.证明函数![]() 是奇函数;求数列
是奇函数;求数列![]() 的通项公式;令
的通项公式;令![]() N
N![]() , 证明:当
, 证明:当![]() 时,
时,![]() .
.
(本小题主要考查函数、数列、不等式等知识, 考查化归与转化、分类与整合的数学思想方法,以及抽象概括能力、推理论证能力、运算求解能力和创新意识)
查看习题详情和答案>> (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。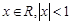 时,有如下表达式:
时,有如下表达式:  两边同时积分得:
两边同时积分得: