摘要:22. 解:(Ⅰ). ----2分 由.得. 当时..单调递减, 当时..单调递增. ----------4分 ∴ 当时.取得最小值. 即对.常数.都有成立. 所以.在上有下界. -----------------6分 (Ⅱ)由.知 -------8分 由.知.. 所以.当.即时..在上单调递增, .即恒成立.在上是有界函数, 当.即时..在上单调递减,.即恒成立.在上是有界函数,------11分 当.即时.有在上单调递减,在上单调递增.且. 从而当时..恒成立.在上是有界函数, 当时..恒成立.在上是有界函数. -----------------------13分 综上可知.在上是有界函数. 且当时.下界为,当时.下界为,当时.下界为. ------------------------------14分
网址:http://m.1010jiajiao.com/timu_id_4032536[举报]
(本题满分14分)已知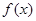 是定义在
是定义在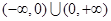 上的奇函数,当
上的奇函数,当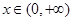 时,
时,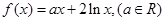
(1)求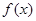 的解析式;
的解析式;
(2)是否存在负实数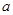 ,使得当
,使得当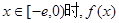 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出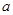 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(3)对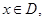 如果函数
如果函数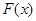 的图像在函数
的图像在函数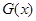 的图像的下方,则称函数
的图像的下方,则称函数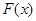 在D上被函数
在D上被函数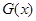 覆盖.求证:若
覆盖.求证:若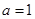 时,函数
时,函数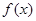 在区间
在区间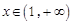 上被函数
上被函数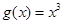 覆盖.
覆盖.
查看习题详情和答案>>
(本题满分14分)
为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
|
|
喜爱打篮球 |
不喜爱打篮球 |
合计 |
|
男生 |
|
5 |
|
|
女生 |
10 |
|
|
|
合计 |
|
|
50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为 .
.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由;
(3)已知喜爱打篮球的10位女生中, 还喜欢打羽毛球,
还喜欢打羽毛球, 还喜欢打乒乓球,
还喜欢打乒乓球, 还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求
还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求 和
和 不全被选中的概率.
不全被选中的概率.
下面的临界值表供参考:
|
|
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
|
|
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: ,其中
,其中
查看习题详情和答案>>
(本题满分14分)已知 是定义在
是定义在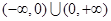 上的奇函数,当
上的奇函数,当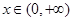 时,
时,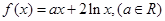
(1)求 的解析式;
的解析式;
(2)是否存在负实数 ,使得当
,使得当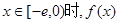 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出 的值;如果不存在,请说明理由.
的值;如果不存在,请说明理由.
(3)对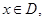 如果函数
如果函数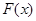 的图像在函数
的图像在函数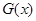 的图像的下方,则称函数
的图像的下方,则称函数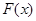 在D上被函数
在D上被函数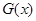 覆盖.求证:若
覆盖.求证:若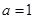 时,函数
时,函数 在区间
在区间 上被函数
上被函数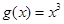 覆盖.
覆盖.


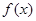 是定义在
是定义在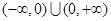 上的奇函数,当
上的奇函数,当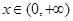 时,
时,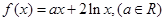
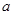 ,使得当
,使得当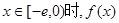 的最小值是4?如果存在,求出
的最小值是4?如果存在,求出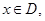 如果函数
如果函数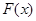 的图像在函数
的图像在函数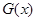 的图像的下方,则称函数
的图像的下方,则称函数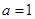 时,函数
时,函数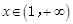 上被函数
上被函数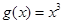 覆盖.
覆盖.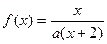 ,方程
,方程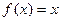 有唯一解,已知
有唯一解,已知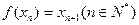 ,且
,且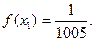
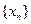 的通项公式;
的通项公式;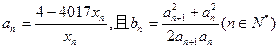 ,求和
,求和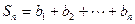 ;
;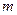 ,使得对任意
,使得对任意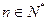 ,有
,有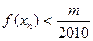 成立,若存在;求出
成立,若存在;求出