摘要：函数零点的概念: 对于函数.把使成立的实数叫做函数的零点． 函数零点的意义: 函数的零点就是方程实数根.亦即函数的图象与轴交点的横坐标． 即: 方程有实数根函数的图象与轴有交点函数有零点． 函数零点的求法: 求函数的零点: ①求方程的实数根, ②对于不能用求根公式的方程.可以将它与函数的图象联系起来.并利用函数的性质找出零点．1．师:引导学生仔细体会左边的这段文字.感悟其中的思想方法． 生:认真理解函数零点的意义.并根据函数零点的意义探索其求法: ①代数法, ②几何法．
网址：http://m.1010jiajiao.com/timu_id_4031719[举报]
（本题满分12分）
已知二次函数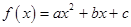
（1）若
，试判断函数
零点个数
(2) 若对
且
，
，证明方程
必有一个实数根属于
(3)是否存在
，使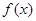
同时满足以下条件①当
时， 函数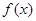有最小值0；；②对
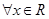,都有
。若存在，求出
的值，若不存在，请说明理由。
查看习题详情和答案>>
已知
，设
和
是方程
的两个根，不等式
对任意实数
恒成立；
函数
有两个不同的零点.求使“P且Q”为真命题的实数
的取值范围.
【解析】本试题主要考查了命题和函数零点的运用。由题设x1＋x2＝a，x1x2＝－2，
∴|x1－x2|＝
＝
.
当a∈[1,2]时，的最小值为3. 当a∈[1,2]时，的最小值为3.
要使|m－5|≤|x1－x2|对任意实数a∈[1,2]恒成立，只须|m－5|≤3，即2≤m≤8.
由已知，得f(x)＝3x2＋2mx＋m＋
＝0的判别式
Δ＝4m2－12(m＋)＝4m2－12m－16>0，
得m<－1或m>4.
可得到要使“P∧Q”为真命题，只需P真Q真即可。
解：由题设x1＋x2＝a，x1x2＝－2，
∴|x1－x2|＝＝.
当a∈[1,2]时，的最小值为3.
要使|m－5|≤|x1－x2|对任意实数a∈[1,2]恒成立，只须|m－5|≤3，即2≤m≤8.
由已知，得f(x)＝3x2＋2mx＋m＋＝0的判别式
Δ＝4m2－12(m＋)＝4m2－12m－16>0，
得m<－1或m>4.
综上，要使“P∧Q”为真命题，只需P真Q真，即
解得实数m的取值范围是(4,8]
查看习题详情和答案>>