摘要：2．先来观察几个具体的一元二次方程的根及其相应的二次函数的图象: ①方程与函数 ②方程与函数 ③方程与函数
网址：http://m.1010jiajiao.com/timu_id_4031717[举报]
某股份公司公开发行4170万股股票，现共有1652158人申购，每人申购1000股，现由计算机按申购先后次序给每个申购者一个编号，并在公证处监督下摇号决定中签号码．若申购者的编号的未位数(或末几位数)与中签号相同者可以购买股票，问应摇出几个不同的一位数，几个不同的二位数，……，几个不同的七位数?
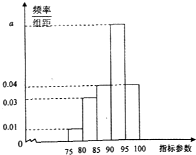（2012•衡阳模拟）针对频繁发生的校车事故，2011年12月27日，工信部发布公告，公开征求对新制订的有关校车安全的几个条例的意见，我市为了了解实际情况，随机抽取了 100辆校车进行检测，将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图．（1）由图中数据，求a的值；
（2）若要从指标参数在[85，90）、[90，95）、[95，100]的三组校车中，用分层抽样方法抽取8辆，作另一项指标脚定，求各组分别抽取的车辆数；
（3）某学校根据自己的实际情况，从（2）中抽取的8辆校车中再随机选4辆来考察校车的价格，设指标参数在[90，95）内的校车被选取的辆数为ξ，求ξ的分布列以及ξ的数学期望．
下表给出的是某港口在某季节每天几个时刻的水深．
（1）若该港口的水深y（m）和时刻t（0≤t≤24）的关系可用函数y=Asin（ωt）+b（其中A＞0，ω＞0，b∈R）来近似描述，求A，ω，b的值；
（2）若一条货船的吃水深度（船底与水面的距离）为4m，安全条例规定至少要有2.5m的安全间隙（船底与海底的距离），试用（1）中的函数关系判断该船何时能进入港口？
查看习题详情和答案>>
| 时刻 | 0：00 | 3：00 | 6：00 | 9：00 | 12：00 | 15：00 | 18：00 | 21：00 | 24：00 |
| 水深/m | 5.0 | 8.0 | 5.0 | 2.0 | 5.0 | 8.0 | 5.0 | 2.0 | 5.0 |
（2）若一条货船的吃水深度（船底与水面的距离）为4m，安全条例规定至少要有2.5m的安全间隙（船底与海底的距离），试用（1）中的函数关系判断该船何时能进入港口？
俗话说“一石激起千层浪”，小时候在水上打“水漂”的游戏一定不会忘记吧．现在一个圆形波浪实验水池的中心已有两个振动源，在t秒内，它们引发的水面波动可分别由函数y1=sin t和y2=sin（t+
）来描述，当这两个振动源同时开始工作时，要使原本平静的水面保持平静，则需再增加一个振动源（假设不计其他因素，则水面波动由几个函数的和表达），请你写出这个新增振动源的函数解析式
．
查看习题详情和答案>>
| 2π | 3 |
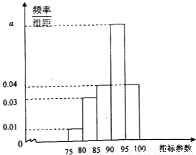针对频繁发生的校车事故，2011年12月27日，工信部发布公告，公开征求对新制订的有关校车安全的几个条例的意见，我市为了了解实际情况，随机抽取了 100辆校车进行检测，将这些校车检測的某项指标参数绘制成如图所示的频率分布直方图．（1）由图中数据，求a的值；
（2）若要从指标参数在[85，90）、[90，95）、[95，100]的三组校车中，用分层抽样方法抽取8辆，作另一项指标脚定，求各组分别抽取的车辆数；
（3）某学校根据自己的实际情况，从（2）中抽取的8辆校车中再随机选4辆来考察校车的价格，设指标参数在[90，95）内的校车被选取的辆数为ξ，求ξ的分布列以及ξ的数学期望．
查看习题详情和答案>>