摘要：2．基本不等式 定理1:如果.那么(当且仅当时取“ ). 说明:(1)指出定理适用范围:,(2)强调取“ 的条件. 定理2:如果是正数.那么(当且仅当时取“= ) 说明:(1)这个定理适用的范围:,(2)我们称的算术平均数.称的几何平均数.即:两个正数的算术平均数不小于它们的几何平均数.
网址：http://m.1010jiajiao.com/timu_id_4030600[举报]
计算
的最值时，我们可以将
化成
=
，再将分式分解成
+
，然后利用基本不等式求最值；借此，计算使得
≥
对一切实数x都成立的正实数c的范围是
查看习题详情和答案>>
| x2+8 | ||
|
| x2+8 | ||
|
| x2+4+4 | ||
|
(
| ||
|
| x2+4 |
| 4 | ||
|
| x2+1+c | ||
|
| 1+c | ||
|
[1，+∞）
[1，+∞）
．（2006•宝山区二模）给出函数f(x)=
+tx（x∈R）．
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
时，可以将f（x）化成f(x)=a(
+x)+b(
-x)的形式，运用基本不等式求f（x）的最小值及此时x的取值；
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
+h(x)，利用基本不等式研究函数F（x）的最值问题．
查看习题详情和答案>>
| x2+4 |
（1）当t≤-1时，证明y=f（x）是单调递减函数；
（2）当t=
| 1 |
| 2 |
| x2+4 |
| x2+4 |
（3）设一元二次函数g（x）的图象均在x轴上方，h（x）是一元一次函数，记F(x)=
| g(x) |
下列结论中，错用基本不等式做依据的是（ ）
A、a，b均为负数，则
| ||||
B、
| ||||
C、sinx+
| ||||
D、a∈R+，(3-a)(1-
|
，求函数 
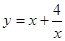的最小值，并求此时x的值.
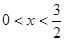，求函数 
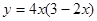的最大值.