摘要：3．等比数列的性质 ①等比数列任意两项间的关系:如果是等比数列的第项.是等差数列的第项.且.公比为.则有, ②对于等比数列.若.则.也就是:.如图所示:. ③若数列是等比数列.是其前n项的和..那么..成等比数列. 如下图所示:
网址：http://m.1010jiajiao.com/timu_id_4030580[举报]
对于任意的n∈N*，若数列{an}同时满足下列两个条件，则称数列{an}具有“性质m”：
①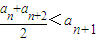
； ②存在实数M，使得an≤M成立．
（1）数列{an}、{bn}中，an=n、
（n=1，2，3，4，5），判断{an}、{bn}是否具有“性质m”；
（2）若各项为正数的等比数列{cn}的前n项和为Sn，且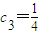
，
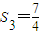，证明：数列{Sn}具有“性质m”，并指出M的取值范围；
（3）若数列{dn}的通项公式
（n∈N*）．对于任意的n≥3（n∈N*）．
查看习题详情和答案>>
①
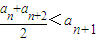； ②存在实数M，使得an≤M成立．（1）数列{an}、{bn}中，an=n、
（n=1，2，3，4，5），判断{an}、{bn}是否具有“性质m”；（2）若各项为正数的等比数列{cn}的前n项和为Sn，且
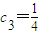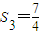，，证明：数列{Sn}具有“性质m”，并指出M的取值范围；（3）若数列{dn}的通项公式
（n∈N*）．对于任意的n≥3（n∈N*）．查看习题详情和答案>>
设x1、x2是区间D上的任意两点，若函数y=f(x)满足f(
成立,则称函数y=f(x)在区间D上下凸.
成立,则称函数y=f(x)在区间D上下凸.(1)证明函数f(x)=x+
在区间(0,+∞)上下凸.
(2)若函数y=f(x)在区间D上下凸,则对任意的x1,x2,…,xn∈D 有
.试根据下凸倒数的这一性质,证明若x1,x2,…,xn∈(0,+∞),则(x1+x2+…+xn)
≥n2.
(文)已知Sn是等比数列{an}的前n项和,且a3,a9,a6成等差数列,问:S3,S9,S6是否成等差数列?
查看习题详情和答案>>（2013•普陀区二模）对于任意的n∈N*，若数列{an}同时满足下列两个条件，则称数列{an}具有“性质m”：
①
＜an+1； ②存在实数M，使得an≤M成立．
（1）数列{an}、{bn}中，an=n、bn=2sin
（n=1，2，3，4，5），判断{an}、{bn}是否具有“性质m”；
（2）若各项为正数的等比数列{cn}的前n项和为Sn，且c3=
，S3=
，证明：数列{Sn}具有“性质m”，并指出M的取值范围；
（3）若数列{dn}的通项公式dn=
（n∈N*）．对于任意的n≥3（n∈N*）．
查看习题详情和答案>>
①
| an+an+2 |
| 2 |
（1）数列{an}、{bn}中，an=n、bn=2sin
| nπ |
| 6 |
（2）若各项为正数的等比数列{cn}的前n项和为Sn，且c3=
| 1 |
| 4 |
| 7 |
| 4 |
（3）若数列{dn}的通项公式dn=
| t (3•2n-n)+1 |
| 2n |
（2013•普陀区二模）对于任意的n∈N*，若数列{an}同时满足下列两个条件，则称数列{an}具有“性质m”：
①
＜an+1；
②存在实数M，使得an≤M成立．
（1）数列{an}、{bn}中，an=n、bn=2sin
（n=1，2，3，4，5），判断{an}、{bn}是否具有“性质m”；
（2）若各项为正数的等比数列{cn}的前n项和为Sn，且c3=
，S3=
，求证：数列{Sn}具有“性质m”；
（3）数列{dn}的通项公式dn=
（n∈N*）．对于任意n∈[3，100]且n∈N*，数列{dn}具有“性质m”，求实数t的取值范围．
查看习题详情和答案>>
①
| an+an+2 |
| 2 |
②存在实数M，使得an≤M成立．
（1）数列{an}、{bn}中，an=n、bn=2sin
| nπ |
| 6 |
（2）若各项为正数的等比数列{cn}的前n项和为Sn，且c3=
| 1 |
| 4 |
| 7 |
| 4 |
（3）数列{dn}的通项公式dn=
| t (3•2n-n)+1 |
| 2n |
； 
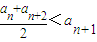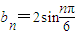（n=1，2，3，4，5），判断{an}、{bn}是否具有“性质m”；
，
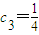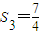，求证：数列{Sn}具有“性质m”；
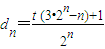（n∈N*）．对于任意n∈[3，100]且n∈N*，数列{dn}具有“性质m”，求实数t的取值范围．