题目内容
对于任意的n∈N*,若数列{an}同时满足下列两个条件,则称数列{an}具有“性质m”:①
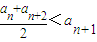 ;
; ②存在实数M,使得an≤M成立.
(1)数列{an}、{bn}中,an=n、
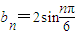 (n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;
(n=1,2,3,4,5),判断{an}、{bn}是否具有“性质m”;(2)若各项为正数的等比数列{cn}的前n项和为Sn,且
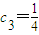 ,
,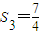 ,求证:数列{Sn}具有“性质m”;
,求证:数列{Sn}具有“性质m”;(3)数列{dn}的通项公式
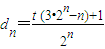 (n∈N*).对于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,求实数t的取值范围.
(n∈N*).对于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,求实数t的取值范围.
【答案】分析:(1)在数列{an}中,令n=1可验证不满足条件①;在数列{bn}中,按“性质m”的定义验证条件①②即可;
(2)将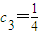 代入S3=
代入S3=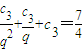 可求得q,从而求得cn,Sn,利用放缩法可验证数列{Sn}满足
可求得q,从而求得cn,Sn,利用放缩法可验证数列{Sn}满足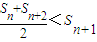 及Sn<2;
及Sn<2;
(3)写出dn+1,dn+2,数列{dn}具有“性质m”,由条件①得dn+dn+2<2dn+1恒成立,代入后化简分离出t,转化为最值问题可得t的范围,在该范围下可判断数列{dn}为递增数列,从而可知{dn}最大项的值为d100,由此知存在M满足条件②,从而得知t的范围;
解答:(1)解:在数列{an}中,取n=1,则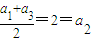 ,不满足条件①,
,不满足条件①,
所以数列{an}不具有“m性质”;
在数列{bn}中,b1=1,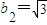 ,b3=2,
,b3=2,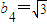 ,b5=1,
,b5=1,
则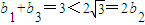 ,
,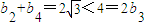 ,
,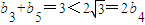 ,所以满足条件①;
,所以满足条件①;
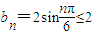 (n=1,2,3,4,5)满足条件②,
(n=1,2,3,4,5)满足条件②,
所以数列{bn}具有“性质m”.
(2)证明:由于数列{cn}是各项为正数的等比数列,则公比q>0,
将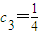 代入S3=
代入S3=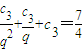 ,得6q2-q-1=0,解得
,得6q2-q-1=0,解得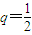 或
或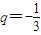 (舍去),
(舍去),
所以c1=1,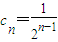 ,
,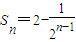 ,
,
对于任意的n∈N*,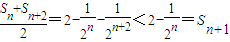 ,且Sn<2,
,且Sn<2,
所以数列{Sn}满足条件①和②,所以数列{Sn}具有“m性质”;
(3)由于dn=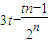 ,则
,则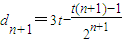 ,
,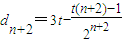 ,
,
由于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,所以dn+dn+2<2dn+1,
即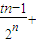
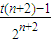
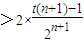 ,
,
化简得,t(n-2)>1,即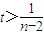 对于任意n∈[3,100]且n∈N*恒成立,
对于任意n∈[3,100]且n∈N*恒成立,
所以t>1①,
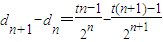 =
=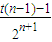 ,
,
由于n∈[3,100]及①,
所以dn+1>dn,即n∈[3,100]时,数列{dn}是单调递增数列,
所以{dn}最大项的值为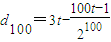 ,
,
满足条件②只需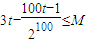 即可,所以这样的M存在②,
即可,所以这样的M存在②,
所以t>1即可.
点评:本题考查等差数列、等比数列的综合,考查学生综合运用所学知识分析问题解决新问题的能力,考查学生对题目的阅读理解能力,对能力要求较高.
(2)将
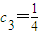 代入S3=
代入S3=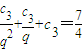 可求得q,从而求得cn,Sn,利用放缩法可验证数列{Sn}满足
可求得q,从而求得cn,Sn,利用放缩法可验证数列{Sn}满足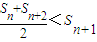 及Sn<2;
及Sn<2;(3)写出dn+1,dn+2,数列{dn}具有“性质m”,由条件①得dn+dn+2<2dn+1恒成立,代入后化简分离出t,转化为最值问题可得t的范围,在该范围下可判断数列{dn}为递增数列,从而可知{dn}最大项的值为d100,由此知存在M满足条件②,从而得知t的范围;
解答:(1)解:在数列{an}中,取n=1,则
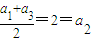 ,不满足条件①,
,不满足条件①,所以数列{an}不具有“m性质”;
在数列{bn}中,b1=1,
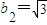 ,b3=2,
,b3=2,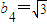 ,b5=1,
,b5=1,则
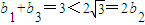 ,
,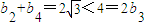 ,
,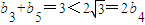 ,所以满足条件①;
,所以满足条件①;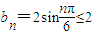 (n=1,2,3,4,5)满足条件②,
(n=1,2,3,4,5)满足条件②,所以数列{bn}具有“性质m”.
(2)证明:由于数列{cn}是各项为正数的等比数列,则公比q>0,
将
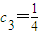 代入S3=
代入S3=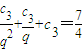 ,得6q2-q-1=0,解得
,得6q2-q-1=0,解得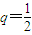 或
或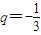 (舍去),
(舍去),所以c1=1,
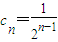 ,
,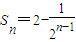 ,
,对于任意的n∈N*,
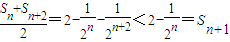 ,且Sn<2,
,且Sn<2,所以数列{Sn}满足条件①和②,所以数列{Sn}具有“m性质”;
(3)由于dn=
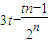 ,则
,则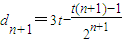 ,
,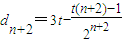 ,
,由于任意n∈[3,100]且n∈N*,数列{dn}具有“性质m”,所以dn+dn+2<2dn+1,
即
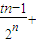
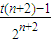
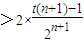 ,
,化简得,t(n-2)>1,即
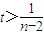 对于任意n∈[3,100]且n∈N*恒成立,
对于任意n∈[3,100]且n∈N*恒成立,所以t>1①,
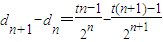 =
=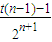 ,
,由于n∈[3,100]及①,
所以dn+1>dn,即n∈[3,100]时,数列{dn}是单调递增数列,
所以{dn}最大项的值为
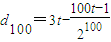 ,
,满足条件②只需
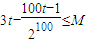 即可,所以这样的M存在②,
即可,所以这样的M存在②,所以t>1即可.
点评:本题考查等差数列、等比数列的综合,考查学生综合运用所学知识分析问题解决新问题的能力,考查学生对题目的阅读理解能力,对能力要求较高.

练习册系列答案
相关题目