摘要:2.探索并掌握等差数列的通项公式与前n项和的公式,
网址:http://m.1010jiajiao.com/timu_id_4030570[举报]
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
查看习题详情和答案>>
bn=
| 等差数列{an} | 等比数列{bn} | ||
| an=a1+(n-1)d | bn=b1qn-1 | ||
| an=am+(n-m)d | bn | ||
若cn=
则数列{cn}为等差数列 |
若dn= 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn=______,dn=______
查看习题详情和答案>>
bn=______,dn=______
| 等差数列{an} | 等比数列{bn} | ||
| an=a1+(n-1)d | bn=b1qn-1 | ||
| an=am+(n-m)d | bn______ | ||
若cn=
则数列{cn}为等差数列 |
若dn=______, 则数列{dn}为等比数列 |
已知等差数列{an}的首项为4,公差为4,其前n项和为Sn,则数列 {![]() }的前n项和为( )
}的前n项和为( )
|
| A. |
| B. |
| C. |
| D. |
|
| 考点: | 数列的求和;等差数列的性质. |
| 专题: | 等差数列与等比数列. |
| 分析: | 利用等差数列的前n项和即可得出Sn,再利用“裂项求和”即可得出数列 { |
| 解答: | 解:∵Sn=4n+ ∴ ∴数列 { 故选A. |
| 点评: | 熟练掌握等差数列的前n项和公式、“裂项求和”是解题的关键. |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
查看习题详情和答案>>
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn=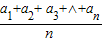 , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
查看习题详情和答案>>
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn= , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |