题目内容
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn=______,dn=______
bn=______,dn=______
| 等差数列{an} | 等比数列{bn} | ||
| an=a1+(n-1)d | bn=b1qn-1 | ||
| an=am+(n-m)d | bn______ | ||
若cn=
则数列{cn}为等差数列 |
若dn=______, 则数列{dn}为等比数列 |
∵等比数列通常与等差数列类比,
加法类比为乘法,
平面中的面积类比为体积,
算术平均数类比为几何平均数
∴bn=bmqn-m,
dn=
,
故选Bmqn-m;
加法类比为乘法,
平面中的面积类比为体积,
算术平均数类比为几何平均数
∴bn=bmqn-m,
dn=
| n | b1b2…bn |
故选Bmqn-m;
| n | b1b2…bn |

练习册系列答案
相关题目
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn=
| 等差数列{an} | 等比数列{bn} | ||
| an=a1+(n-1)d | bn=b1qn-1 | ||
| an=am+(n-m)d | bn | ||
若cn=
则数列{cn}为等差数列 |
若dn= 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn=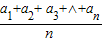 , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn=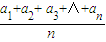 , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |
类比是一个伟大的引路人.我们知道,等差数列和等比数列有许多相似的性质,请阅读下表并根据等差数列的结论,类似的得出等比数列的两个结论:
bn= ,dn=
bn= ,dn=
| 等差数列{an} | 等比数列{bn} |
| an=a1+(n-1)d | bn=b1qn-1 |
| an=am+(n-m)d | bn |
若cn= , ,则数列{cn}为等差数列 | 若dn= , 则数列{dn}为等比数列 |