摘要：2．线面垂直 定义:如果一条直线l和一个平面α相交.并且和平面α内的任意一条直线都垂直.我们就说直线l和平面α互相垂直其中直线l叫做平面的垂线.平面α叫做直线l的垂面,直线与平面的交点叫做垂足.直线l与平面α垂直记作:l⊥α. 直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直.那么这条直线垂直于这个平面. 直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行.
网址：http://m.1010jiajiao.com/timu_id_4030330[举报]
平面几何中，同垂直于一条直线的两直线________.那么，类比到空间中有：（1）同垂直于一条直线的两条直线平行,这个命题成立吗？______.为什么？_______.（2）同垂直于一个平面的两条直线_________.这个命题是__________（填：真、假）命题.原因是：已知a⊥平面α,b⊥平面α,求证：a∥b.假设b不平行于a,设b∩α=O,b′是经过点O与直线_______平行的直线.∵a_______b′,a⊥α ,?∴b′________α,?即经过同一点O的两条直线________、_______都垂直于平面α，这是不可能的.因此，________.这种证明的方法是________法.?
命题（2）的逆命题是：如果两条平行直线中的一条垂直于一个平面，那么另一条也_________这个平面.用数学符号表示：已知a_____b,a_______平面α,求证：b______α.?
证明：设m是α内的任意一条直线.∵a________α,m
α,?
?∴a________m.又∵a_______b,∴________bm.又∵m
α,m是_______,∴由线面垂直的__________可知b______α.
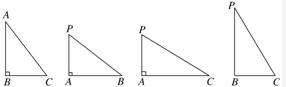13、下面一组图形为三棱锥P-ABC的底面与三个侧面．已知AB⊥BC，PA⊥AB，PA⊥AC．（1）写出三棱锥P-ABC中的所有的线面垂直关系（不要求证明）；
（2）在三棱锥P-ABC中，求证：平面ABC⊥平面PAB．
（2012•莆田模拟）如图，AB⊥BC，BC⊥CD，AB=BC=CD=1，AD=| 3 |
（1）请观察图形直接写出两对不同的线面垂直关系，并任选其中一对加以证明；
（2）试求直线BD与平面BEF所成的角的大小．
如图所示，圆柱的高为2，底面半径为
,AE、DF是圆柱的两条母线，过
作圆柱的截面交下底面于
.
（1）求证：
；
（2）若四边形ABCD是正方形，求证
；
（3）在（2）的条件下，求二面角A-BC-E的平面角的一个三角函数值。
【解析】第一问中，利用由圆柱的性质知：AD平行平面ＢＣＦＥ
又过作圆柱的截面交下底面于.
∥
又AE、DF是圆柱的两条母线
∥ＤＦ，且ＡＥ＝ＤＦ 
ＡＤ∥ＥＦ
第二问中，由线面垂直得到线线垂直。四边形ABCD是正方形
又
BC、AE是平面ABE内两条相交直线
第三问中，设正方形ABCD的边长为x,则在
在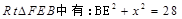
由（2）可知：
为二面角A-BC-E的平面角，所以
证明：（1）由圆柱的性质知：AD平行平面ＢＣＦＥ
又过作圆柱的截面交下底面于.∥
又AE、DF是圆柱的两条母线
∥ＤＦ，且ＡＥ＝ＤＦ ＡＤ∥ＥＦ
(2)
四边形ABCD是正方形 又
BC、AE是平面ABE内两条相交直线
(3)设正方形ABCD的边长为x,则在
在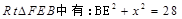
由（2）可知：为二面角A-BC-E的平面角，所以
查看习题详情和答案>>