题目内容
 (2012•莆田模拟)如图,AB⊥BC,BC⊥CD,AB=BC=CD=1,AD=
(2012•莆田模拟)如图,AB⊥BC,BC⊥CD,AB=BC=CD=1,AD=| 3 |
(1)请观察图形直接写出两对不同的线面垂直关系,并任选其中一对加以证明;
(2)试求直线BD与平面BEF所成的角的大小.
分析:(1)由图形可得CD⊥平面ABC,AB⊥平面BCD.证明AC⊥CD,根据BC⊥CD,AC∩BC=C,可得CD⊥平面ABC,从而可得CD⊥AB,根据AB⊥BC,BC∩CD=C,可得AB⊥平面BCD;
(2)建立空间直角坐标系,求出平面BEF的法向量
=(1,0,1),利用向量的夹角公式,即可求直线BD与平面BEF所成的角的大小.
(2)建立空间直角坐标系,求出平面BEF的法向量
| n |
解答:解:(1)由图形可得CD⊥平面ABC,AB⊥平面BCD.下面证明AB⊥平面BCD:
在△ABC中,AB⊥BC,AB=BC=1,∴AC=
在△ACD中,CD=1,AC=
,AD=
,∴AD2=AC2+DC2,∴AC⊥CD
∵BC⊥CD,AC∩BC=C
∴CD⊥平面ABC
∵AB?平面ABC
∴CD⊥AB
∵AB⊥BC,BC∩CD=C
∴AB⊥平面BCD;
(2)以C为原点,BC所在直线为x轴,CD所在直线为y轴,建立如图所示的空间直角坐标系
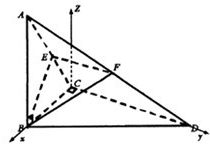
则A(1,0,1),B(1,0,0),C(0,0,0),D(0,1,0),E(
,0,
),F(
,
,
)
设平面BEF的法向量为
=(x,y,z),直线BD与平面BEF所成的角为θ
∵
=(
,0,
),
=(
,
,
)
∴
,∴可取
=(1,0,1)
∵
=(-1,0,1)
∴sinθ=
=
=
.
∵θ∈[0,
]
∴θ=
在△ABC中,AB⊥BC,AB=BC=1,∴AC=
| 2 |
在△ACD中,CD=1,AC=
| 2 |
| 3 |
∵BC⊥CD,AC∩BC=C
∴CD⊥平面ABC
∵AB?平面ABC
∴CD⊥AB
∵AB⊥BC,BC∩CD=C
∴AB⊥平面BCD;
(2)以C为原点,BC所在直线为x轴,CD所在直线为y轴,建立如图所示的空间直角坐标系

则A(1,0,1),B(1,0,0),C(0,0,0),D(0,1,0),E(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
设平面BEF的法向量为
| n |
∵
| BE |
| 1 |
| 2 |
| 1 |
| 2 |
| BF |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
| n |
∵
| BD |
∴sinθ=
|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∵θ∈[0,
| π |
| 2 |
∴θ=
| π |
| 6 |
点评:本题考查线面垂直,考查线面角,解题的关键是掌握线面垂直的判定,正确运用空间向量解决线面角问题,属于中档题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 (2012•莆田模拟)如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论:
(2012•莆田模拟)如图,F是抛物线E:y2=2px(p>0)的焦点,A是抛物线E上任意一点.现给出下列四个结论: