摘要：函数图象的几何特征与函数性质的数量特征紧密结合.有效地揭示了各类函数和定义域.值域.单调性.奇偶性.周期性等基本属性.体现了数形结合的特征与方法.为此.既要从定形.定性.定理.定位各方面精确地观察图形.绘制图形.又要熟练地掌握函数图象的平移变换.对称变换. 常见的函数数字特征有: (1)函数奇偶性: 奇函数, 偶函数. (2)函数单调性: 单调递增或, 单调递增或. (3)函数周期性 周期为:或, (4)对称性 关于y轴对称:, 关于原点对称:, 关于直线对称:或, 关于点对称:或.
网址：http://m.1010jiajiao.com/timu_id_4030271[举报]
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}（1）将“特征数”是{0，
| ||
| 3 |
y=
x-1
| ||
| 3 |
y=
x-1
； （答案写在答卷上）
| ||
| 3 |
（2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=
| 3 |
（3）若（2）中的四边形与“特征数”是{1，-2b，b2+
| 1 |
| 2 |
定义{a，b，c}为函数y=ax2+bx+c的“特征数”．如：函数y=x2-2x+3的“特征数”是{1，-2，3}，函数y=2x+3的“特征数”是{0，2，3，}，函数y=-x的“特征数”是{0，-1，0}
（1）将“特征数”是{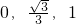
}的函数图象向下平移2个单位，得到的新函数的解析式是________； （答案写在答卷上）
（2）在（1）中，平移前后的两个函数分别与y轴交于A、B两点，与直线x=
分别交于D、C两点，在平面直角坐标系中画出图形，判断以点A、B、C、D为顶点的四边形形状，并说明理由；
（3）若（2）中的四边形与“特征数”是{
}的函数图象的有交点，求满足条件的实数b的取值范围．
查看习题详情和答案>>
函数y=sin（ωx+?）（ω＞0，0＜?＜π）为偶函数，该函数的部分图象如图所示，A、B分别为最高点与最低点，并且
我市沿海某医药研究所开发一种新药，如果成年人按规定的剂量服用，据监测，服药后每毫升血液中的含药量y（微克）与时间t（小时）之间近似满足如图所示的曲线（OA为线段，AB为某二次函数图象的一部分，B是抛物线顶点，O为原点）．（Ⅰ）写出服药后y与t之间的函数关系式y=f（t）；
（Ⅱ）据进一步测定：每毫升血液中含药量不少于
| 4 | 9 |
（2012•黄浦区二模）对n∈N*，定义函数fn（x）=-（x-n）2+n，n-1≤x≤n．
（1）求证：y=fn（x）图象的右端点与y=fn+1（x）图象的左端点重合；并回答这些端点在哪条直线上．
（2）若直线y=knx与函数fn（x）=-（x-n）2+n，n-1≤x≤n（n≥2，n∈N*）的图象有且仅有一个公共点，试将kn表示成n的函数．
（3）对n∈N*，n≥2，在区间[0，n]上定义函数y=f（x），使得当m-1≤x≤m（n∈N*，且m=1，2，…，n）时，f（x）=fm（x）．试研究关于x的方程f（x）=fn（x）（0≤x≤n，n∈N*）的实数解的个数（这里的kn是（2）中的kn），并证明你的结论．
查看习题详情和答案>>
（1）求证：y=fn（x）图象的右端点与y=fn+1（x）图象的左端点重合；并回答这些端点在哪条直线上．
（2）若直线y=knx与函数fn（x）=-（x-n）2+n，n-1≤x≤n（n≥2，n∈N*）的图象有且仅有一个公共点，试将kn表示成n的函数．
（3）对n∈N*，n≥2，在区间[0，n]上定义函数y=f（x），使得当m-1≤x≤m（n∈N*，且m=1，2，…，n）时，f（x）=fm（x）．试研究关于x的方程f（x）=fn（x）（0≤x≤n，n∈N*）的实数解的个数（这里的kn是（2）中的kn），并证明你的结论．