摘要:3.最值 (1)定义: 最大值:一般地.设函数y=f(x)的定义域为I.如果存在实数M满足:①对于任意的x∈I.都有f(x)≤M,②存在x0∈I.使得f(x0) = M.那么.称M是函数y=f(x)的最大值. 最小值:一般地.设函数y=f(x)的定义域为I.如果存在实数M满足:①对于任意的x∈I.都有f(x)≥M,②存在x0∈I.使得f(x0) = M.那么.称M是函数y=f(x)的最大值. 注意: 1 函数最大(小)首先应该是某一个函数值.即存在x0∈I.使得f(x0) = M, 2 函数最大(小)应该是所有函数值中最大(小)的.即对于任意的x∈I.都有f(x)≤M(f(x)≥M). (2)利用函数单调性的判断函数的最大(小)值的方法: 1 利用二次函数的性质求函数的最大(小)值, 2 利用图象求函数的最大(小)值, 3 利用函数单调性的判断函数的最大(小)值: 如果函数y=f(x)在区间[a.b]上单调递增.在区间[b.c]上单调递减则函数y=f(x)在x=b处有最大值f(b), 如果函数y=f(x)在区间[a.b]上单调递减.在区间[b.c]上单调递增则函数y=f(x)在x=b处有最小值f(b),
网址:http://m.1010jiajiao.com/timu_id_4030240[举报]
(1)最值的定义:在闭区间上函数的最大的函数值叫函数的__________,最小的函数值叫函数的___________.?
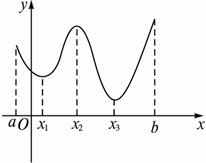
(2)观察右面一个定义在闭区间[a,b]上的函数y=f(x)的图象:?
极大值有_______,最大值为________;?
极小值有_______,最小值为________.
查看习题详情和答案>>