摘要：“函数 是数学中最重要的概念之一.学习函数的概念首先要掌握函数三要素的基本内容与方法.由给定函数解析式求其定义域这类问题的代表.实际上是求使给定式有意义的x的取值范围它依赖于对各种式的认识与解不等式技能的熟练.1．求函数解析式的题型有: (1)已知函数类型.求函数的解析式:待定系数法, (2)已知求或已知求:换元法.配凑法, (3)已知函数图像.求函数解析式, (4)满足某个等式.这个等式除外还有其他未知量.需构造另个等式:解方程组法, (5)应用题求函数解析式常用方法有待定系数法等.
网址：http://m.1010jiajiao.com/timu_id_4030232[举报]
定义函数f（x）=
，给出下列四个命题：
（1）该函数的值域为[-1，1]；
（2）当且仅当x=2kπ+
（k∈Z）时，该函数取得最大值；
（3）该函数是以π为最小正周期的周期函数；
（4）当且仅当2kπ+π＜x＜2kπ+
（k∈Z）时，f（x）＜0．上述命题中正确的个数是
查看习题详情和答案>>
|
（1）该函数的值域为[-1，1]；
（2）当且仅当x=2kπ+
| π |
| 2 |
（3）该函数是以π为最小正周期的周期函数；
（4）当且仅当2kπ+π＜x＜2kπ+
| 3π |
| 2 |
1个
1个
．定义函数f(x)=
，给出下列四个命题：①该函数的值域是[-2，2]；②该函数是以π为最小正周期的周期函数；③当且仅当x=2kπ-
(k∈Z)时该函数取得最大值2；④当且仅当2kπ-π＜x＜2kπ-
(k∈Z)时，f（x）＜0．上述命题中，错误命题的个数是（ ）
|
| π |
| 2 |
| π |
| 2 |
查看习题详情和答案>>
对于函数f（x）=
，给出下列四个命题：
①该函数的值域为[-1，1]；
②当且仅当x=2kπ+
（k∈z）时，该函数取得最大值1；
③该函数是以π为最小正周期的周期函数；
④当且仅当2kπ+π＜x＜2kπ+
（k∈z）时，f（x）＜0．
上述命题中错误命题的个数为（ ）
|
①该函数的值域为[-1，1]；
②当且仅当x=2kπ+
| π |
| 2 |
③该函数是以π为最小正周期的周期函数；
④当且仅当2kπ+π＜x＜2kπ+
| 3π |
| 2 |
上述命题中错误命题的个数为（ ）
| A、1 | B、2 | C、3 | D、4 |
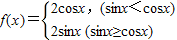，给出下列四个命题：①该函数的值域是[-2，2]；②该函数是以π为最小正周期的周期函数；③当且仅当
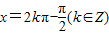时该函数取得最大值2；④当且仅当
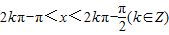时，f（x）＜0．上述命题中，错误命题的个数是（ ）