Question

（2008•青浦区一模）定义函数f(x)=

sinx，sinx≥cosx cosx，sinx＜cosx

，
给出下列四个命题：
（1）该函数的值域为[-1，1]；
（2）当且仅当x=2kπ+

π

2

(k∈Z)时，该函数取得最大值；
（3）该函数是以π为最小正周期的周期函数；
（4）当且仅当2kπ+π＜x＜2kπ+

3π

2

(k∈Z)时，f（x）＜0．
上述命题中正确的个数是（　　）

A．1个

B．2个

C．3个

D．4个

Answer 1

分析：由题意可得：函数 f(x)=

sinx，[2kπ+ π 4 ，2kπ+ 5π 4 ] cosx，[2kπ- 3π 4 ，2kπ+ π 4 ]

，再根据周期函数的定义结合其图象可得函数的周期等性质即可．

解答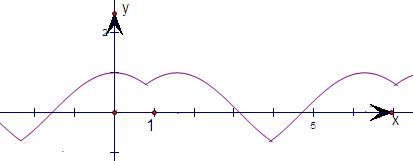：解：由题意可得：函数 f(x)=

sinx当sinx≥cosx时 cosx当sinx＜cosx时

，即 f(x)=

sinx，[2kπ+ π 4 ，2kπ+ 5π 4 ] cosx，[2kπ- 3π 4 ，2kπ+ π 4 ]

，作出其图象如图，从图象上可以看出：
（1）该函数的值域为[-

2

2

，1]；故（1）错；
（2）当且仅当x=2kπ+

π

2

(k∈Z)或x=2kπ（k∈Z）时，该函数取得最大值；帮（2）错；
（3）该函数是以2π为最小正周期的周期函数；（3）错；
（4）当且仅当2kπ+π＜x＜2kπ+

3π

2

(k∈Z)时，f（x）＜0，（4）正确．
故选A．

点评：本题主要考查三角函数的有关性质，如周期性，单调性，最值等性质，考查运算求解能力，属于基础题．