题目内容
定义函数f(x)=
,给出下列四个命题:
(1)该函数的值域为[-1,1];
(2)当且仅当x=2kπ+
(k∈Z)时,该函数取得最大值;
(3)该函数是以π为最小正周期的周期函数;
(4)当且仅当2kπ+π<x<2kπ+
(k∈Z)时,f(x)<0.上述命题中正确的个数是
|
(1)该函数的值域为[-1,1];
(2)当且仅当x=2kπ+
| π |
| 2 |
(3)该函数是以π为最小正周期的周期函数;
(4)当且仅当2kπ+π<x<2kπ+
| 3π |
| 2 |
1个
1个
.分析:f(x)为分段函数,由已知分别解出自变量的范围,从而求得f(x)的值域为[-
,1],f(x)取得最大值1时,得x=
+2kπ或x=2kπ(k∈Z),求解f(x)的最小正周期周期,利用定义f(x+T)=f(x)来判断,计算出π不是f(x)的最小正周期,经过验证第四个命题是对的.
| ||
| 2 |
| π |
| 2 |
解答:解:∵sinx≥cosx,∴
+2kπ≤x≤
+2kπ
∵sinx<cosx,∴-
+2kπ<x<
+2kπ
∴f(x)=
,∴f(x)的值域为[-
,1]
当x=
+2kπ或x=2kπ(k∈Z)时,f(x)取得最大值为1.
∵f(x+π)=
≠f(x)
∴f(x)不是以π为最小正周期的周期函数,
当f(x)<0时,2kπ+π<x<2kπ+
(k∈Z)
综上所述,正确的个数是1个,
故答案为1个.
| π |
| 4 |
| 5π |
| 4 |
∵sinx<cosx,∴-
| 3π |
| 4 |
| π |
| 4 |
∴f(x)=
|
| ||
| 2 |
当x=
| π |
| 2 |
∵f(x+π)=
|
∴f(x)不是以π为最小正周期的周期函数,
当f(x)<0时,2kπ+π<x<2kπ+
| 3π |
| 2 |
综上所述,正确的个数是1个,
故答案为1个.
点评:本题主要考查求解三角函数的值域、周期、最值等知识,是三角函数的基础知识,应熟练掌握.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t). 已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t).
已知二次函数f(x)=3x2-3x直线l1:x=2和l2:y=3tx,其中t为常数且0<<1.直线l2与函数f(x)的图象以及直线l1、l2与函数f(x)的图象围成的封闭图形如图中阴影所示,设这两个阴影区域的面积之和为S(t). sinx,cosx),
sinx,cosx), =(cosx,-cosx),x∈R,定义函数f(x)=
=(cosx,-cosx),x∈R,定义函数f(x)=
 ,f(C)=0,若向量
,f(C)=0,若向量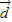 =(1,sinA)与
=(1,sinA)与  =(2,sinB)共线,求边a,b的值及△ABC的面积S?
=(2,sinB)共线,求边a,b的值及△ABC的面积S?