摘要： 已知函数f(x)=x3+x 证明: 是增函数; (2) 若a,b,c∈R, 且,a+b>0,b+c>0,c+a>0,则f>0. 证明:(1)设x1<x2 f(x1)-f(x2)=x13+x1-x23-x2 =(x1-x2)(x12+x1x2+x22+1) ① 当x1,x2同号时, ①=(x1-x2)[(x1-x2)2+3x1x2+1)]<0 当x1,x2异号时,①=(x1-x2)[(x1+x2)2-x1x2+1)]<0 综上有f(x1)<f(x2),故f(x)是增函数. , ∴f(x)是奇函数.又a+b>0即a>-b ∴f,即 f>0. 同理, f+f(c)>0. 三式相加得2[f]>0,所以f>0成立.
网址：http://m.1010jiajiao.com/timu_id_4028164[举报]
已知函数f(x)=x3-ax-1.
（1）若f(x)在实数集R上单调递增，求实数a的取值范围；
（2）是否存在实数a，使f(x)在（-1，1）上单调递减？若存在，求出a的取值范围，若不存在，请说明理由；
（3）证明f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
查看习题详情和答案>>已知函数f(x)=x3-ax-1.
(1)若f(x)在实数集R上单调递增，求实数a的取值范围；
（2）是否存在实数a,使f(x)在（-1，1）上单调递减？若存在，求出a的取值范围；若不存在，说明理由；
（3）证明：f(x)=x3-ax-1的图象不可能总在直线y=a的上方.
查看习题详情和答案>>
已知函数f(x)=x3-xn2+
+
且存在x0∈(0,
),使f(x0)=x0.
+且存在x0∈(0,),使f(x0)=x0.(1)证明f(x)是R上的单调增函数;
设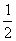
其中,n=1,2,….
(2)证明xn＜xn+1＜x0＜yn+1＜yn;
(3)证明
.