题目内容

已知函数f(x)=x3-xn2++且存在x0∈(0,),使f(x0)=x0.

(1)证明f(x)是R上的单调增函数;

设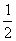

其中,n=1,2,….

(2)证明xn＜xn+1＜x0＜yn+1＜yn;

(3)证明.

思路分析:本小题主要考查函数、导数及其应用等基本知识,考查运用数学知识分析和解决实际问题的能力.

证明:(1)∵f′(x)=3x2-2x+=3(x-)2+＞0,

∴f(x)是R上的单调增函数.

(2)∵0＜x0＜,即x1＜x0＜y1.

又f(x)是增函数,∴f(x1)＜f(x0)＜f(y1),即x2＜x0＜y2.

又x2=f(x1)=f(0)=＞0=x1,y2=f(y1)=f()=＜=y1,综上,x1＜x2＜x0＜y2＜y1.

用数学归纳法证明如下:

①当n=1时,上面已证明成立.

②假设当n=k(k≥1)时,有xk＜xk+1＜x0＜yk+1＜yk.

当n=k+1时,由f(x)是单调增函数,有f(xk)＜f(xk+1)＜f(x0)＜f(yk+1)＜f(yk),

∴xk+1＜xk+2＜x0＜yk+2＜yk+1.

由①②知对一切n=1,2,…,都有xn＜xn+1＜x0＜yn+1＜yn.

(3)=yn2+xnyn+xn2-(yn+xn)+≤(yn+xn)2-(yn+xn)+

=［(yn+xn)-］2+.

由(2)知0＜yn+xn＜1.

∴-＜yn+xn-＜.

∴＜()2+=.

练习册系列答案
相关题目
已知函数f(x)=x-2m2+m+3(m∈Z)为偶函数，且f（3）＜f（5）．
（1）求m的值，并确定f（x）的解析式；
（2）若g（x）=loga[f（x）-ax]（a＞0且a≠1），是否存在实数a，使g（x）在区间[2，3]上的最大值为2，若存在，请求出a的值，若不存在，请说明理由．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．

已知函数f(x)的图像在[a，b]上连续不断，f1(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f2(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f2(x)－f1(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x2，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．
已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f（x）、g（x），下列说法正确的是（ ）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网