摘要：随机变量的数学期望: 一般地.若离散型随机变量ξ的概率分布为 ξ x1 x2 - xn - P p1 p2 - pn - 则称 Eξ=x1p1+x2p2+--+xnpn- 为ξ的数学期望.简称期望.也叫平均数,均值. (1)数学期望是离散型随机变量的一个特征数.它反映了离散型随机变量取值的平均水平. (2)期望的一个性质:E(aξ+b)=aEξ+b (3)求期望的方法步骤: ①确定随机变量的所有取值; ②计算第个取值的概率并列表; ③由期望公式计算期望值. 4. 方差: Dξ=(x1-Eξ)2p1+(x2-Eξ)2p2+-+(xn-Eξ)2pn+- (1) 标准差:Dξ的算术平方根叫做随机变量ξ的标准差.记作 (2)方差的性质: D(aξ+b)=a2Dξ; Dξ=E(ξ2)-(Eξ)2 (3)方差的求法步骤: ①求分布列; ②求期望; ③由公式计算方差. 随机变量的方差与标准差都反映了:随机变量取值的稳定与波动.集中与离散的程度.
网址：http://m.1010jiajiao.com/timu_id_4023676[举报]
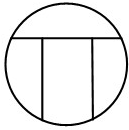（2009•普陀区二模）园丁要用红、黄、蓝、白四种不同颜色的鲜花布置如图所示圆形花坛的四块区域．要求同一区域内须用同一种颜色的鲜花，相邻区域须用不同颜色的鲜花．设花圃中布置红色鲜花的区域数量为ξ，则随机变量ξ的数学期望Eξ1
1
．
某地区对12岁儿童瞬时记忆能力进行调查．瞬时记忆能力包括听觉记忆能力与视觉记忆能力．某班学生共有40人，下表为该班学生瞬时记忆能力的调查结果．例如表中听觉记忆能力为中等，且视觉记忆能力偏高的学生为3人．
由于部分数据丢失，只知道从这40位学生中随机抽取一个，视觉记忆能力恰为中等，且听觉记忆能力为中等或中等以上的概率为
．
（1）试确定a、b的值；
（2）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
（3）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为ξ，求随机变量ξ的数学期望Eξ． 查看习题详情和答案>>
| 听觉 视觉 |
视觉记忆能力 | ||||
| 偏低 | 中等 | 偏高 | 超常 | ||
| 听觉 记忆 能力 |
偏低 | 0 | 7 | 5 | 1 |
| 中等 | 1 | 8 | 3 | b | |
| 偏高 | 2 | a | 0 | 1 | |
| 超常 | 0 | 2 | 1 | 1 | |
| 2 |
| 5 |
（1）试确定a、b的值；
（2）从40人中任意抽取3人，求其中至少有一位具有听觉记忆能力或视觉记忆能力超常的学生的概率；
（3）从40人中任意抽取3人，设具有听觉记忆能力或视觉记忆能力偏高或超常的学生人数为ξ，求随机变量ξ的数学期望Eξ． 查看习题详情和答案>>
（2008•卢湾区一模）（理）袋中有同样的球5个，其中3个红色，2个黄色，现从中随机且不放回地摸球，每次摸1个，当两种颜色的球都被摸到时，即停止摸球，记随机变量ξ为此时已摸球的次数，求：
（1）随机变量ξ的概率分布；
（2）随机变量ξ的数学期望与方差．
查看习题详情和答案>>
（1）随机变量ξ的概率分布；
（2）随机变量ξ的数学期望与方差．