摘要:例4.已知.F椭圆的两个焦点.过点F的直线BC交椭圆于B.C两点. (1).求点M的轨迹方程. [答案] (2)若相应于焦点F的准线与x轴相交于点A.|OF|=2|FA|.过点A的直线与椭圆相交于P.Q两点.设().过点P且平行于准线的直线与椭圆相交于另一点M.证明:. 解:(1)略 (2) 证明:.由已知得方程组 注意.解得 因.故 . 而.所以 . [结论发散]设P()为椭圆上一点. (1)求的Min (2)求的Max (3)当<0时.的取值范围. (4)若相应于焦点F的准线与x轴相交于点A..求 (5)已知点M的坐标为(2,3).求的最值. (6)已知点Q的坐标为(1,1).求的最小值 (7)已知点Q的坐标为(1,1).求的最值 [提示] = =2a+2a+=2a+ 例5.已知A.B为抛物线上两点.直线AB过焦点F.A.B在准线上的射影分别为C.D. (1) 若.求抛物线的方程. (2) CD是否恒存在一点K.使得 Y A F P B X O D K C 解:(1)提示:记A().B ()设直线AB方程为代入抛物线方程得 (2)设线段AB中点P在在准线上的射影为T. 则 =-=-=0 故存在点K即点T.使得 [实质:以AB为直径的圆与准线相切] [结论发散1] y轴上是否恒存在一点K.使得 [实质:以AF为直径的圆与y轴相切] [结论发散2]求证: [结论发散3]求证:存在实数使得 [实质:证明A.O.D三点共线] [结论发散4] 设线段AB中点P在在准线上的射影为T.证明: [题设变更1] 已知A.B为抛物线上两点..点C坐标为 (1) 求证:∥ (2)若=()且试求点M的轨迹方程. [题设变更2]如图.过抛物线x2=4y的对称轴上任一点P作直线与抛物线交于A.B两点.点Q是点P关于原点的对称点.设点P分有向线段所成的比为.证明:, 解:依题意.可设直线AB的方程为 代入抛物线方程得 ① 设A.B两点的坐标分别是 ..x2是方程①的两根. 所以 由点P(0.m)分有向线段所成的比为. 得 又点Q是点P关于原点的对称点. 故点Q的坐标是.从而. 所以 思维能力训练
网址:http://m.1010jiajiao.com/timu_id_4023500[举报]
已知F是椭圆 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线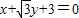 相切.
相切.
(1)求椭圆的方程;
(2)设O为椭圆的中心,过F点作直线交椭圆于M、N两点,在椭圆上是否存在点T,使得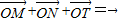 ,如果存在,则求点T的坐标;如果不存在,请说明理由.
,如果存在,则求点T的坐标;如果不存在,请说明理由.
 查看习题详情和答案>>
查看习题详情和答案>>
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线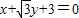 相切.
相切.(1)求椭圆的方程;
(2)设O为椭圆的中心,过F点作直线交椭圆于M、N两点,在椭圆上是否存在点T,使得
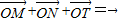 ,如果存在,则求点T的坐标;如果不存在,请说明理由.
,如果存在,则求点T的坐标;如果不存在,请说明理由. 查看习题详情和答案>>
查看习题详情和答案>>
已知F是椭圆 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线 相切.
相切.
(Ⅰ)求椭圆的方程;
(Ⅱ)设O为椭圆的中心,是否存在过F点,斜率为k(k∈R,l≠0)且交椭圆于M、N两点的直线,当从O点引出射线经过MN的中点P,交椭圆于点Q时,有 成立.如果存在,则求k的值;如果不存在,请说明理由.
成立.如果存在,则求k的值;如果不存在,请说明理由.
查看习题详情和答案>>
 的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为
的左焦点,A是椭圆短轴上的一个顶点,椭圆的离心率为 ,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线
,点B在x轴上,AB⊥AF,A、B、F三点确定的圆C恰好与直线 相切.
相切.(Ⅰ)求椭圆的方程;
(Ⅱ)设O为椭圆的中心,是否存在过F点,斜率为k(k∈R,l≠0)且交椭圆于M、N两点的直线,当从O点引出射线经过MN的中点P,交椭圆于点Q时,有
 成立.如果存在,则求k的值;如果不存在,请说明理由.
成立.如果存在,则求k的值;如果不存在,请说明理由.查看习题详情和答案>>
已知点F是椭圆
+y2=1(a>0)右焦点,点M(m,0)、N(0,n)分别是x轴、y轴上的动点,且满足
•
=0,若点P满足
=2
+
.
(1)求P点的轨迹C的方程;
(2)设过点F任作一直线与点P的轨迹C交于A、B两点,直线OA、OB与直线x=-a分别交于点S、T(其中O为坐标原点),试判断
•
是否为定值?若是,求出这个定值;若不是,请说明理由.
查看习题详情和答案>>
| x2 |
| 1+a2 |
| MN |
| NF |
| OM |
| ON |
| PO |
(1)求P点的轨迹C的方程;
(2)设过点F任作一直线与点P的轨迹C交于A、B两点,直线OA、OB与直线x=-a分别交于点S、T(其中O为坐标原点),试判断
| FS |
| FT |