摘要:掌握公式形式特征.能正用.逆用和变形运用.会 “添拆项 凑定值和等号成立的条件.
网址:http://m.1010jiajiao.com/timu_id_4023487[举报]
已知数列{an}的首项为1,f(n)=a1
+a2
+…+ak
+…+an
(n∈N+).
(1)若{an}为常数列,求f(4)的值;
(2)若{an}为公比为2的等比数列,求f(n)的解析式;
(3)数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立.若能,求出数列{an}的通项公式;若不能,试说明理由.
查看习题详情和答案>>
| C | 1 n |
| C | 2 n |
| C | k n |
| C | n n |
(1)若{an}为常数列,求f(4)的值;
(2)若{an}为公比为2的等比数列,求f(n)的解析式;
(3)数列{an}能否成等差数列,使得f(n)-1=(n-1)2n对一切n∈N+都成立.若能,求出数列{an}的通项公式;若不能,试说明理由.
已知α,β∈R且αβ≠0,数列{xn}满足x1=α+β,x2=α2+αβ+β2,xn+2=(α+β)xn+1-αβ•xn(n≥1,n∈N),令bn=xn+1-αxn.
(1)求证:{bn}是等比数列;
(2)求数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)若α=β=
,求{xn}的前n项和Sn.
查看习题详情和答案>>
(1)求证:{bn}是等比数列;
(2)求数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)若α=β=
| 1 | 2 |
设数列{an}中,a1=a,an+1+2an=2n+1(n∈N*).
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列{
-
}能否为等比数列.若是等比数列,请写出相应数列{an}的通项公式;若不能,请说明理由.
查看习题详情和答案>>
(Ⅰ)若a1,a2,a3成等差数列,求实数a的值;
(Ⅱ)试问数列{
| an |
| 2n |
| 1 |
| 2 |
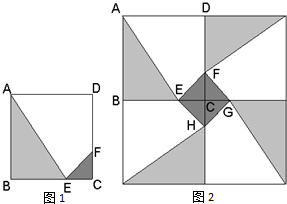 某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=
某人定制了一批地砖,每块地砖 (如图1所示)是边长为40cm的正方形ABCD,点E,F分别在边BC和CD上,△CFE,△ABE和四边形AEFD均由单一材料制成,制成△CFE,△ABE和四边形AEFD的三种材料的每平方米价格之比依次为3:2:1.若将此种地砖按图2所示的形式铺设,能使中间的深色阴影部分构成四边形EFGH.则当CE=