题目内容
已知α,β∈R且αβ≠0,数列{xn}满足x1=α+β,x2=α2+αβ+β2,xn+2=(α+β)xn+1-αβ•xn(n≥1,n∈N),令bn=xn+1-αxn.
(1)求证:{bn}是等比数列;
(2)求数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)若α=β=
,求{xn}的前n项和Sn.
(1)求证:{bn}是等比数列;
(2)求数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)若α=β=
| 1 | 2 |
分析:(1)利用已知条件,推出
是常数,即可证明{bn}是等比数列;
(2)通过α≠β与α=β,分别求出数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)利用(2)的结论,通过α=β=
,写出{xn}的通项公式,利用错位相减法求出前n项和Sn.
| bn+1 |
| bn |
(2)通过α≠β与α=β,分别求出数列{xn}的通项公式;(不能直接使用竞赛书上的结论,要有推导过程)
(3)利用(2)的结论,通过α=β=
| 1 |
| 2 |
解答:解:(1)因为bn=xn+1-αxn.
所以b1=x2-αx1=α2+αβ+β2-α(α+β)=β2.
=
=β.所以{bn}是等比数列;
(2)①当α≠β时,∴xn-αxn-1=β(xn-1-αxn-2),xn-βxn-1=α(xn-1-βxn-2),
由等比数列性质可得,
xn-αxn-1=(x2-αx1)βn-2=βn,
xn-βxn-1=(x2-βx1)αn-2=αn,
联立解得:xn=
,
②当α=β时,由①可得,xn-αxn-1=(x2-αx1)βn-2,
∵α=β,xn-αxn-1=(x2-αx1)αn-2=αn,即xn=αxn-1+αn,
等式两边同除以αn,得:
=
+1
即
-
=1,
数列{
}是以1为公差的等差数列,
=
+(n-1)×1=
+n-1=n+1,
xn=(n+1)αn
综上所述,xn=
…(10分)
(3)因为α=β=
,由(2)可得xn=(n+1)•(
)n
Sn=[(
) +(
)2+(
)3+…+(
)n ]+[(
) +2×(
)2+3×(
)3+…+n×(
)n ],
令P=1×
+2×(
)2+3×(
)3+…+n×(
)n,…①
P=(
)2+2×(
)3+3×(
)4+…+n×(
)n+1…②,
①-②得,
P=
+(
)2+(
)3+…+(
)n-n ×(
)n+1=1-(
)n-n ×(
)n+1.
∴Sn=1-(
)n+2-(
)n-1-n(
)n=3-(n+3)(
)n…(14分)
所以b1=x2-αx1=α2+αβ+β2-α(α+β)=β2.
| bn+1 |
| bn |
| xn+2-αxn+1 |
| xn+1- αxn |
(2)①当α≠β时,∴xn-αxn-1=β(xn-1-αxn-2),xn-βxn-1=α(xn-1-βxn-2),
由等比数列性质可得,
xn-αxn-1=(x2-αx1)βn-2=βn,
xn-βxn-1=(x2-βx1)αn-2=αn,
联立解得:xn=
| αn+1-βn+1 |
| α-β |
②当α=β时,由①可得,xn-αxn-1=(x2-αx1)βn-2,
∵α=β,xn-αxn-1=(x2-αx1)αn-2=αn,即xn=αxn-1+αn,
等式两边同除以αn,得:
| xn |
| αn |
| xn-1 |
| αn-1 |
即
| xn |
| αn |
| xn-1 |
| αn-1 |
数列{
| xn |
| αn |
| xn |
| αn |
| x1 |
| α |
| 2α |
| α |
xn=(n+1)αn
综上所述,xn=
|
(3)因为α=β=
| 1 |
| 2 |
| 1 |
| 2 |
Sn=[(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
令P=1×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴Sn=1-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查数列的判定,数列通项公式与前n项和的求法,考查分类讨论思想,计算能力.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
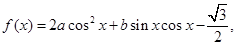 x∈R且
x∈R且 ,
,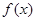 的最小正周期;
的最小正周期;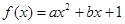 (
(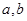 ∈R且
∈R且 ),
),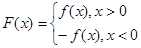 .
. ,且函数
,且函数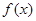 的值域为[0, +
的值域为[0, +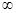 ),求
),求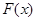 的解析式;
的解析式; 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;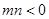 ,
,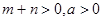 , 且
, 且 是否大于零?
是否大于零? (
(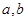 ∈R且
∈R且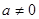 ),
),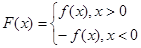 .
. ,且函数
,且函数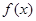 的值域为[0, +
的值域为[0, +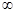 ),求
),求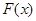 的解析式;
的解析式;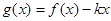 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;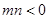 ,
,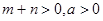 , 且
, 且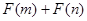 能否大于零?
能否大于零?