摘要:20.已知函数. (1)求函数的单调区间, (2)设.求在上的最大值, (3)试证明:对任意.不等式恒成立. 解:(1)∵ 令得 显然是上方程的解 令..则 ∴函数在上单调递增 ∴是方程的唯一解 ∵当时.当时 ∴函数在上单调递增.在上单调递减------5分 知函数在上单调递增.在上单调递减 故①当即时在上单调递增 ∴= ②当时在上单调递减 ∴= ③当.即时 --------------------10分 知当时. ∴在上恒有.当且仅当时“= 成立 ∴对任意的恒有 ∵ ∴ 即对.不等式恒成立.---------14分
网址:http://m.1010jiajiao.com/timu_id_4021289[举报]
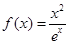 .
.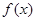 的单调区间;
的单调区间;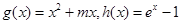 ,若在
,若在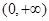 上至少存在一点
上至少存在一点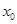 ,使得
,使得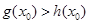 成立,求
成立,求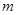 的范围.
的范围. .
.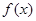 的单调区间;
的单调区间;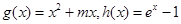 ,若在
,若在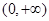 上至少存在一点
上至少存在一点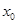 ,使得
,使得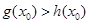 成立,求
成立,求 的范围.
的范围.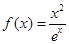 .
.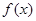 的单调区间;
的单调区间;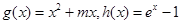 ,若在
,若在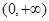 上至少存在一点
上至少存在一点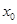 ,使得
,使得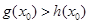 成立,求
成立,求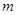 的范围.
的范围.