摘要：作为一堂概念课.学生对于概念的理解必须精确.深入.为后续课程打下扎实的基础.教师必须在这一环节进行深入的分析. 因此.在圆以及曲线的参数方程的概念引入之后.针对参数方程的形式.参数的取值范围.参数方程与普通方程的统一性.参数的作用以及参数的意义进行深入的理解与探讨.通过这一环节.学生活跃的思维逐步从感性上升到理性,同时.对于概念的理解得到巩固与深化. 通过加强师生交流.关注学生思维.把握课堂教学重点.让学生体验知识产生的原因.发展的过程及其应用的价值.
网址：http://m.1010jiajiao.com/timu_id_4019897[举报]
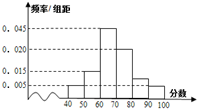某校对参加数学竞赛的学生中随机选取40名学生的成绩作为样本，这40名学生的成绩全部在40分到100之间，现将成绩按如下方式分成6组，即：[40，50），[50，60），[60，70），[70，80），[80，90），[90，100]据此绘制如图所示的频率直方图，在选取的40名学生中（1）求成绩在区间[80，90）内的学生人数；
（2）从成绩大于等于80分的学生中，随机选两名学生，求至少有一名学生成绩在区间[90，100]内的概率．
2006年6月，世界杯足球赛决赛在德国拉开战幕，6月5日，某班40名学生就哪支队伍将夺冠进行竞猜，统计结果如图．若把认为巴西队将夺冠的这组学生人数作为一组的频数，则这一组的频率为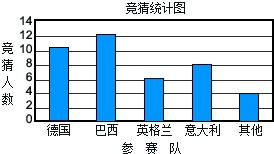
．
查看习题详情和答案>>
（8分）对某校高一年级学生参加社区服务次数进行统计，随机抽取
名学生作为样本，得到这名学生参加社区服务的次数．根据此数据作出了频数与频率的统计表和频率分布直方图如下：
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
25 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
M |
1 |
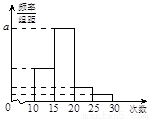
⑴求出表中、
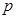及图中
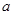的值；
⑵若该校高一学生有720人，试估计他们参加社区服务的次数在区间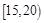
内的人数；
⑶在所取样本中，从参加社区服务的次数不少于20次的学生中任选2人，求至多一人参加社区服务次数在区间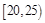
内的概率.
查看习题详情和答案>>
名学生作为样本，得到这
及图中
的值；
内的人数；
内的概率.
