题目内容
(8分)对某校高一年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
25 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
M |
1 |
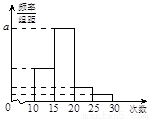
⑴求出表中 、
、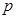 及图中
及图中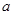 的值;
的值;
⑵若该校高一学生有720人,试估计他们参加社区服务的次数在区间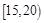 内的人数;
内的人数;
⑶在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间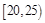 内的概率.
内的概率.
⑴ ,
,  =0.125,p=3\40;⑵;⑶
=0.125,p=3\40;⑵;⑶
【解析】
试题分析:⑴由题可知 ,
,  ,
,  ,
,  .
.
又  ,解得
,解得  ,
, ,
, ,
, .
.
则 组的频率与组距之比
组的频率与组距之比 为0.125.
为0.125.
⑵参加在社区服务次数在区间 内的人数为
内的人数为 人.
人.
⑶在样本中,处于 内的人数为3,可分别记为
内的人数为3,可分别记为 ,处于
,处于 内的人数为2,可分别记为
内的人数为2,可分别记为 . 从该5名同学中取出2人的取法有
. 从该5名同学中取出2人的取法有
 共10种;至多一人在
共10种;至多一人在 内的情况有
内的情况有 共7种,所以至多一人参加社区服务次数在区间
共7种,所以至多一人参加社区服务次数在区间 内的概率为
内的概率为 .
.
考点:频率分布直方图;频率分布表;用样本的频率分布估计总体分布;随机事件的概率。
点评:本题考查频率分布直方图,考查阅读图像,信息提取,处理数据的能力.在频率分布直方图中,小长方形的面积就是这组数据的频率。属于基础题型。

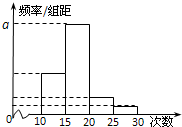 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表如下,频率分布直方图如图:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | a |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
(Ⅱ)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间[10,15)内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间[20,25)内的概率.
本小题满分12分)
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
|
分组 |
频数 |
频率 |
|
|
10 |
0.25 |
|
|
25 |
|
|
|
|
|
|
|
2 |
0.05 |
|
合计 |
M |
1 |

(Ⅰ)求出表中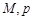 及图中
及图中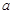 的值;
的值;
(Ⅱ)若该校高一学生有360人,试估计该校高一学生参加社区服务的次数在区间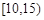 内的人数;
内的人数;
(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间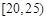 内的概率.
内的概率.







 (2012•湖北模拟)对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此教据作出了频数与频率的统计表和频率分布直方图:
(2012•湖北模拟)对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数根据此教据作出了频数与频率的统计表和频率分布直方图:



