摘要：10．如图.在平面直角坐标系xOy中.A(a,0)(a>0).B(0.a).C.D(0,4).设△AOB的外接圆圆心为E. (1)若⊙E与直线CD相切.求实数a的值, (2)设点P在圆E上.使△PCD的面积等于12的点P有且只有三个.试问这样的⊙E是否存在.若存在?求出⊙E的标准方程,若不存在.说明理由． 解:(1)直线CD方程为y＝x+4.圆心E(.).半径r＝a. 由题意得＝a.解得a＝4. (2)∵|CD|＝＝4.∴当△PCD面积为12时.点P到直线CD的距离为3.又圆心E到直线CD距离为2.要使△PCD的面积等于12的点P有且只有三个.只须圆E半径＝5.解得a＝10. 此时.⊙E的标准方程为(x-5)2+(y-5)2＝50.
网址：http://m.1010jiajiao.com/timu_id_4015945[举报]
如图，在平面直角坐标系xOy中，A（1，0），B（1，1），C（0，1），映射f将xOy平面上的点P（x，y）对应到另一个平面直角坐标系uO'v上的点P'（2xy，x2-y2），则当点P沿着折线A-B-C运动时，在映射f的作用下，动点P'的轨迹是（ ）A、 | B、 | C、 | D、 |
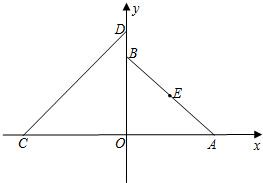如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（-4，0），D（0，4），设△AOB的外接圆为⊙E．（1）若⊙E与直线CD相切，求实数a的值；
（2）问是否存在这样的⊙E，⊙E上到直线CD的距离为3
| 2 |
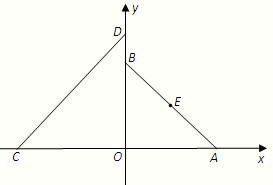如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（-4，0），D（0，4），设△AOB的外接圆圆心为E．（1）问圆心E到直线CD的距离是否为定值，若是，求出定值；若不是，说明理由；
（2）问当a取何值时，圆E与直线CD相切，并求出此时⊙E的标准方程．
如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（-4，0）D（0，4）设△AOB的外接圆圆心为E．
如图，在平面直角坐标系xOy中，A（a，0）（a＞0），B（0，a），C（-4，0），D（0，4），设△AOB的外接圆为⊙E．
的点P有且只有三个；若存在，求出⊙E的标准方程；若不存在，请说明理由．