摘要：总结出的表格 图象的特征 函数的性质 (1)图象都在轴的右边 点 (2)1的对数是0 (3)从左往右看.当＞1时.图象逐渐上升.当0＜＜1时.图象逐渐下降 . (3)当＞1时.是增函数.当 0＜＜1时.是减函数. (4)当＞1时.函数图象在(1.0)点右边的纵坐标都大于0.在(1.0)点左边的纵坐标都小于0. 当0＜＜1时.图象正好相反.在(1.0)点右边的纵坐标都小于0.在(1.0)点左边的纵坐标都大于0 . (4)当＞1时 ＞1.则＞0 0＜＜1.＜0 当0＜＜1时 ＞1.则＜0 0＜＜1.＜0
网址：http://m.1010jiajiao.com/timu_id_4013053[举报]
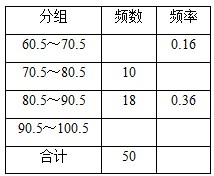2008年的汶川大地震震撼了大家的心灵．在地震后大家发现，学习了防震知识且训练有素的学校的师生在地震中伤亡很小；相反的，没有这方面准备的学校损失惨重．为了让大家了解更多的防震避灾的知识，某校举行了一次“防震知识竞赛”，共有800名学生参加了这次竞赛．为了了解本次竞赛成绩的情况，从中抽取了部分学生的成绩进行统计．但是操作人员不小心将频率分布表局部污损，根据这个污损的表格解答下列问题：（1）若用系统抽样的方法抽取50个样本，现将所有学生随机地编号为000，001，002，…，799，
试写出第二组第一位学生的编号；
（2）填充频率分布表的空格（将答案直接填在表格内），并作出频率分布直方图；
（3）若成绩在85.5～95.5分的学生为二等奖，问参赛学生中获得二等奖的学生约为多少人？
若A1，A2，…，Am为集合A={1，2，…，n}（n≥2且n∈N*）的子集，且满足两个条件：
①A1∪A2∪…∪Am=A；
②对任意的{x，y}⊆A，至少存在一个i∈{1，2，3，…，m}，使Ai∩{x，y}={x}或{y}．则称集合组A1，A2，…，Am具有性质P．
如图，作n行m列数表，定义数表中的第k行第l列的数为akl=
．
（Ⅰ）当n=4时，判断下列两个集合组是否具有性质P，如果是请画出所对应的表格，如果不是请说明理由；
集合组1：A1={1，3}，A2={2，3}，A3={4}；
集合组2：A1={2，3，4}，A2={2，3}，A3={1，4}．
（Ⅱ）当n=7时，若集合组A1，A2，A3具有性质P，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合A1，A2，A3；
（Ⅲ）当n=100时，集合组A1，A2，…，At是具有性质P且所含集合个数最小的集合组，求t的值及|A1|+|A2|+…|At|的最小值．（其中|Ai|表示集合Ai所含元素的个数） 查看习题详情和答案>>
①A1∪A2∪…∪Am=A；
②对任意的{x，y}⊆A，至少存在一个i∈{1，2，3，…，m}，使Ai∩{x，y}={x}或{y}．则称集合组A1，A2，…，Am具有性质P．
如图，作n行m列数表，定义数表中的第k行第l列的数为akl=
|
| a11 | a12 | … | a1m |
| a21 | a22 | … | a2m |
| … | … | … | … |
| an1 | an2 | … | anm |
集合组1：A1={1，3}，A2={2，3}，A3={4}；
集合组2：A1={2，3，4}，A2={2，3}，A3={1，4}．
（Ⅱ）当n=7时，若集合组A1，A2，A3具有性质P，请先画出所对应的7行3列的一个数表，再依此表格分别写出集合A1，A2，A3；
（Ⅲ）当n=100时，集合组A1，A2，…，At是具有性质P且所含集合个数最小的集合组，求t的值及|A1|+|A2|+…|At|的最小值．（其中|Ai|表示集合Ai所含元素的个数） 查看习题详情和答案>>
在某次试验中，有两个试验数据x，y统计的结果如下面的表格：| x | 1 | 2 | 3 | 4 | 5 |
| y | 2 | 3 | 4 | 4 | 5 |
（2）用最小二乘法求线性回归方程
| ? |
| y |
| ? |
| b |
| ? |
| a |
（3）根据所求回归方程预测当x=6时y的值．
（2007广州市水平测试）下面是某地100位居民月均用水量的频率分布表：
（1）请同学们完成上面的频率分布表（请把答案填在答卷所提供的表格上）；
（2）根据频率分布表，画出频率分布直方图（请把答案画在答卷所提供的坐标系上）；
（3）根据频率分布表和频率分布直方图估计该地居民月均用水量落在[1，2.5 ）范围内的概率大约是多少？
查看习题详情和答案>>
| 分 组 | 频 数 | 频 率 |
| [0，0.5 ） | 5 | 0.05 |
| [0.5，1 ） | 10 | |
| [1，1.5 ） | 15 | |
| [1.5，2 ） | 20 | |
| [2，2.5 ） | 25 | |
| [2.5，3 ） | 10 | |
| [3，3.5 ） | 8 | |
| [3.5，4 ） | 5 | |
| [4，4.5 ） | 2 | |
| 合计 | 100 | 1.00 |
（2）根据频率分布表，画出频率分布直方图（请把答案画在答卷所提供的坐标系上）；
（3）根据频率分布表和频率分布直方图估计该地居民月均用水量落在[1，2.5 ）范围内的概率大约是多少？
在某次试验中，有两个试验数据x，y，统计的结果如下面的表格