摘要: 对于定义域为的函数.如果同时满足以下三条:①对任意的.总有,②,③若.都有成立.则称函数为理想函数. (1) 若函数为理想函数.求的值, (2)判断函数是否为理想函数.并予以证明, (3)若函数为理想函数.假定.使得.且.求证. 批阅时间 等级 姓名 作业时间: 2010 年 月 日 星期 作业编号 003
网址:http://m.1010jiajiao.com/timu_id_4010166[举报]
对于定义域为![]() 的函数
的函数![]() ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 为理想函数.
为理想函数.
(1) 若函数![]() 为理想函数,求
为理想函数,求![]() 的值;
的值;
(2)判断函数![]() (
(![]() )是否为理想函数,并予以证明;
)是否为理想函数,并予以证明;
对于定义域为 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:
①对任意的 ,总有
,总有 ;②
;② ;③若
;③若 都有
都有 成立;
成立;
则称函数 为
为 函数.
函数.
下面有三个命题:
(1)若函数 为
为 函数,则
函数,则 ;(2)函数
;(2)函数 是
是 函数;
函数;
(3)若函数 为
为 函数,假定存在
函数,假定存在 ,使得
,使得 ,且
,且 ,
则
,
则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号)
查看习题详情和答案>>
对于定义域为 的函数
的函数 ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的 ,总有
,总有 ;②
;② ;③若
;③若 ,都有
,都有 成立,则称函数
成立,则称函数 为理想函数.
为理想函数.
(1) 若函数 为理想函数,求
为理想函数,求 的值;
的值;
(2)判断函数
 是否为理想函数,并予以证明;
是否为理想函数,并予以证明;
(3) 若函数 为理想函数,
为理想函数, 假定
假定
 ,使得
,使得 ,且
,且 ,求证:
,求证: .
.
查看习题详情和答案>>
 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:  ,总有
,总有 ;②
;② ;③若
;③若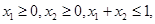 都有
都有 成立;
成立;  函数.
函数.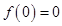 ;(2)函数
;(2)函数 是
是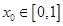 ,使得
,使得 ,且
,且 , 则
, 则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号) 的函数
的函数 ,如果同时满足以下三个条件:
,如果同时满足以下三个条件:  ,总有
,总有 ;②
;② ;③若
;③若 都有
都有 成立;
成立;  函数.
函数. ;(2)函数
;(2)函数 是
是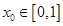 ,使得
,使得 ,且
,且 , 则
, 则 ; 其中真命题是________.(填上所有真命题的序号)
; 其中真命题是________.(填上所有真命题的序号)