题目内容
对于定义域为![]() 的函数
的函数![]() ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的![]() ,总有
,总有![]() ;②
;②![]() ;③若
;③若![]() ,都有
,都有![]() 成立,则称函数
成立,则称函数![]() 为理想函数.
为理想函数.
(1) 若函数![]() 为理想函数,求
为理想函数,求![]() 的值;
的值;
(2)判断函数![]() (
(![]() )是否为理想函数,并予以证明;
)是否为理想函数,并予以证明;
(1)![]() (2)
(2)![]() 理想函数
理想函数
解析:
证明函数![]() (
(![]() )满足三个条件
)满足三个条件
(1)取![]() 可得
可得![]() .
.
又由条件①![]() ,故
,故![]() .
.
(2)显然![]() 在[0,1]满足条件①
在[0,1]满足条件①![]() ;
;
也满足条件②![]() .若
.若![]() ,
,![]() ,
,![]() ,则
,则
![]()
![]() ,即满足条件③,
,即满足条件③,
故![]() 理想函数.
理想函数.

练习册系列答案
相关题目
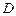 的函数
的函数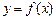 ,若有常数M,使得对任意的
,若有常数M,使得对任意的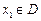 ,存在唯一的
,存在唯一的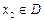 满足等式
满足等式 ,则称M为函数
,则称M为函数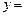 f (x)的“均值”.
f (x)的“均值”.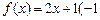 ≤
≤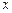 ≤
≤ 的“均值”,请说明理由;
的“均值”,请说明理由;
 为常数)存在“均值”,求实数a的取值范围;
为常数)存在“均值”,求实数a的取值范围; 是单调函数,且其值域为区间I.试探究函数
是单调函数,且其值域为区间I.试探究函数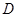 的函数
的函数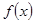 ,若存在区间
,若存在区间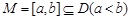 ,使得
,使得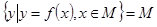 则称区间M为函数
则称区间M为函数 ; ②
; ②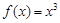 ; ③
; ③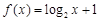
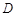 的函数
的函数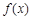 ,如果存在
,如果存在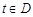 ,使得
,使得 成立,称函数
成立,称函数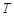 ”函数。已知下列函数:①
”函数。已知下列函数:①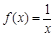 ; ②
; ②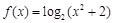 ;③
;③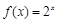 (
(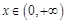 ); ④
); ④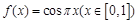 ,其中属于“
,其中属于“