摘要：[例1]证明:当x>0时.有 证明:设f=0． ∵f/(x)=1-cosx处f/(x)=0 ∴当x>0时.f>f(0) 即x-sinx>0, x>sinx 为证不等式.设 g(x)=sinx-x+,则g(0)=0, 于是g/在x>0时递增.从而有g=0 即 故当x>0时有 提炼方法:证不等式的依据I: 在x>a可导.且递增.则f; 在x>a可导.且递减.则f(x)
网址：http://m.1010jiajiao.com/timu_id_4009425[举报]
21、例4．已知f（x）=ax2+bx+c，g（x）=ax+b（a、b、c∈R），当x∈[-1，1]时，|f（x）|≤1
（1）证明：|c|≤1．
（2）x∈[-1，1]时，证明|g（x）|≤2．
（3）设a＞0，当-1≤x≤1时，g（x）max=2，求f（x）．
查看习题详情和答案>>
（1）证明：|c|≤1．
（2）x∈[-1，1]时，证明|g（x）|≤2．
（3）设a＞0，当-1≤x≤1时，g（x）max=2，求f（x）．
已知函数f（x）（x∈R）满足：对于任意实数x，y，都有f(x+y)=f(x)+f(y)+
恒成立，且当x＞0时，f(x)＞-
恒成立；
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
）有三个零点x1，x2，x3，求u=（x1+x2+x3）+x1•x2•x3的取值范围．
查看习题详情和答案>>
| 1 |
| 2 |
| 1 |
| 2 |
（1）求f（0）的值，并例举满足题设条件的一个特殊的具体函数；
（2）判定函数f（x）在R上的单调性，并加以证明；
（3）若函数F（x）=f（max{-x，2x-x2}）+f（-k）+1（其中max{a，b}=
|
|AB|=|xA-xB|表示数轴上A，B两点的距离，它也可以看作满足一定条件的一种运算．这样，可以将满足下列三个条件的一个x与y间的运算p（x，y）叫做x，y之间的距离：条件一，非负性p（x，y）≥0，等号成立当且仅当x=y；条件二，交换律p（x，y）=p（y，x）；条件三，三角不等式p（x，z）≤p（x，y）+p（y，z）．
试确定运算s(x，y)=
是否为一个距离？是，证明；不是，举出反例．
查看习题详情和答案>>
试确定运算s(x，y)=
| |x-y| | 1+|x-y| |
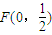，M（0，1），N（0，2）．点P（x，y）在抛物线x2=2y上
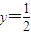所得的弦长；