摘要：了解可导函数的单调性与其导数的关系.会用导数分析函数的单调性.进而求解函数不等式的问题,
网址：http://m.1010jiajiao.com/timu_id_4009414[举报]
（本小题满分12分）
已知函数
；
（1）求
; （2）求
的最大值与最小值.
【解析】第一问利用导数的运算法则，幂函数的导数公式，可得。
第二问中，利用第一问的导数，令导数为零，得到
然后结合导数，函数的关系判定函数的单调性，求解最值即可。
查看习题详情和答案>>
已知函数y=x+
（x＞0）有如下性质：如果常数a＞0，那么该函数在（0，
]上是减函数，在[
，+∞）上是增函数．
（1）如果函数y=x+
（x＞0）的值域为[6，+∞），求b的值；
（2）研究函数y=x2+
（x＞0，常数c＞0）在定义域内的单调性，并用定义证明（若有多个单调区间，请选择一个证明）；
（3）对函数y=x+
和y=x2+
（x＞0，常数a＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数F（x）=(x2+
)2+(
+x)2在区间[
，2]上的最大值和最小值（可利用你的研究结论）．
查看习题详情和答案>>
| a |
| x |
| a |
| a |
（1）如果函数y=x+
| b2 |
| x |
（2）研究函数y=x2+
| c |
| x2 |
（3）对函数y=x+
| a |
| x |
| a |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| 2 |
已知函数y=x+
有如下性质：如果常数a＞0，那么该函数在（0，
]上是减函数，在[
，+∞）上是增函数．
（Ⅰ）如果函数y=x+
（x＞0）的值域为[6，+∞），求b的值；
（Ⅱ）研究函数y=x2+
（常数c＞0）在定义域内的单调性，并说明理由；
（Ⅲ）对函数y=x+
和y=x2+
（常数a＞0）作出推广，使它们都是你所推广的函数的特例．研究推广后的函数的单调性（只须写出结论，不必证明），并求函数F（x）=（x2+
）n+（
+x）n（n是正整数）在区间[
，2]上的最大值和最小值（可利用你的研究结论）．
查看习题详情和答案>>
| a |
| x |
| a |
| a |
（Ⅰ）如果函数y=x+
| 2b |
| x |
（Ⅱ）研究函数y=x2+
| c |
| x2 |
（Ⅲ）对函数y=x+
| a |
| x |
| a |
| x2 |
| 1 |
| x |
| 1 |
| x2 |
| 1 |
| 2 |
＝
＋
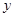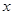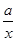有如下性质：如果常数
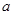＞0，那么该
0，
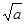
上是减函数，在
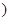上是增函数．
（
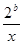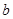的值；
＋
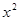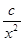（常数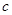
＞0）在定义域内的单调性，并说明理由；
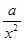（常数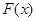
＝
＋
（
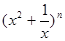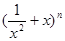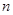是正整数）在区间[
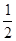，2]上的最大值和最小值（可利用你
=
（
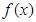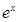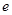为自然对数的底数），
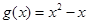，记
．
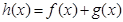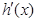为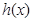
的导函数，判断函数
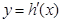的单调性，并加以证明；
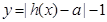=0有两个零点，求实数
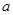的取值范围．