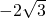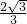摘要： 空间向量. (1)a.共线向量:共线向量亦称平行向量.指空间向量的有向线段所在直线互相平行或重合. (2)空间向量基本定理:如果三个向量不共面.那么对空间任一向量.存在一个唯一的有序实数组x.y.z.使. 推论:设O.A.B.C是不共面的四点.则对空间任一点P, 都存在唯一的有序实数组x.y.z使 . (3)a.空间向量的坐标:空间直角坐标系的x轴是横轴.y轴是纵轴.z轴是竖轴. ①令=,.则 .. . ∥ . . (用到常用的向量模与向量之间的转化: ) 空间两个向量的夹角公式 (a＝.b＝). ②空间两点的距离公式:. b.法向量:若向量所在直线垂直于平面.则称这个向量垂直于平面.记作.如果那么向量叫做平面的法向量. c.用向量的常用方法: ①利用法向量求点到面的距离定理:如图.设n是平面的法向量.AB是平面的一条射线.其中.则点B到平面的距离为. ②.异面直线间的距离 (是两异面直线.其公垂向量为.分别是上任一点.为间的距离). ③.点到平面的距离 (为平面的法向量.是经过面的一条斜线.). ④直线与平面所成角(为平面的法向量). ⑤利用法向量求二面角的平面角定理:设分别是二面角中平面的法向量.则所成的角就是所求二面角的平面角或其补角大小(方向相同.则为补角.反方.则为其夹角). 二面角的平面角或(.为平面.的法向量).

网址：http://m.1010jiajiao.com/timu_id_4008899[举报]