摘要:解:(1)S1=S2+S3---------------------2分 (2)S1.S2.S3之间的关系为:S1=S2+S3----------3分 证明:∵S1= ∴S2+S3=(AC2+AB2) 又:AC2+BC2=AB2 ∴S2+S3=AB2=S1----------------6分 (3)所作的三角形应满足:是以AB.BC.AC为对应边的三个相似三角形--7分 证明:∵=(= ∴S2= 同理:S3= ∴S2+S3==----10分 (4)向形外以AB.BC.AC为对应边作三个相似的图形 则有S1=S2+S3----------------------12分 说明:(3)中只要学生说到相似三角形即可. (4)中同样说明相似图形即可.
网址:http://m.1010jiajiao.com/timu_id_4007546[举报]
(1)如图(1)两个圆中,⊙O1与⊙O2相交于A、B,过B点的直线交两圆于C、D,已知⊙O1与⊙O2的半径分别为6和8,求证:AD:AC的比值为定值;
(2)如图(2),D为线段AB延长线上的一点,△ABC与△BDE都是等边三角形,连接CE并延长,△ABC的外接圆⊙O交CF于M,请解答下列问题:
①求证:BE切⊙O于B;
②若CM=2,MF=6,求⊙O的半径;
③过D作DG∥BE交EF于G,过G作GH∥DE交DF于H,设△ABC、△BDE、△DHG的面积分别为S1、S2、S3,试探究S1、S2、S3之间的关系.

查看习题详情和答案>>
(2)如图(2),D为线段AB延长线上的一点,△ABC与△BDE都是等边三角形,连接CE并延长,△ABC的外接圆⊙O交CF于M,请解答下列问题:
①求证:BE切⊙O于B;
②若CM=2,MF=6,求⊙O的半径;
③过D作DG∥BE交EF于G,过G作GH∥DE交DF于H,设△ABC、△BDE、△DHG的面积分别为S1、S2、S3,试探究S1、S2、S3之间的关系.

如图(1),△ABC中,AD为BC边上的的中线,则![]() .(模拟改编)
.(模拟改编)

实践探究
(1)在图(2)中,E、F分别为矩形ABCD的边AD、BC的中点,则![]() 之间满足的关系式为 ;
之间满足的关系式为 ;
| |
| |
(2)在图(3)中,E、F分别为平行四边形ABCD的边AD、BC的中点,则![]() 之间满足的关系式为
之间满足的关系式为 ![]() ;
;
(3)在图(4)中,E、F分别为任意四边形ABCD的边AD、BC的中点,则![]() 之间满足的关系式为 ;
之间满足的关系式为 ;
解决问题:
(4)在图(5)中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+ S2+ S3+ S4=?
 |
查看习题详情和答案>>
如图(1),△ABC中,AD为BC边上的的中线,则S△ABD=S△ACD。
实践探究
(1)在图(2)中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴影和S矩形ABCD之间满足的关系式为________;
实践探究
(1)在图(2)中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴影和S矩形ABCD之间满足的关系式为________;

(2)在图(3)中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴影和S平行四边形ABCD之间满足的关系式为_______;
(3)在图(4)中,E、F分别为任意四边形ABCD的边AD、BC的中点,则之间满足的关系式为_______;
(3)在图(4)中,E、F分别为任意四边形ABCD的边AD、BC的中点,则之间满足的关系式为_______;
解决问题:
(4)在图(5)中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+ S2+ S3+S4=?
(4)在图(5)中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+ S2+ S3+S4=?

操作示例
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ADC.
实践探究
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为

(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为 ;
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为 ;
解决问题:
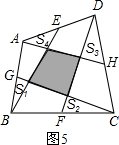
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+S2+S3+S4= .
 查看习题详情和答案>>
查看习题详情和答案>>
如图1,△ABC中,AD为BC边上的中线,则S△ABD=S△ADC.
实践探究
(1)在图2中,E、F分别为矩形ABCD的边AD、BC的中点,则S阴和S矩形ABCD之间满足的关系式为

(2)在图3中,E、F分别为平行四边形ABCD的边AD、BC的中点,则S阴和S平行四边形ABCD之间满足的关系式为
(3)在图4中,E、F分别为任意四边形ABCD的边AD、BC的中点,则S阴和S四边形ABCD之间满足的关系式为
解决问题:
(4)在图5中,E、G、F、H分别为任意四边形ABCD的边AD、AB、BC、CD的中点,并且图中阴影部分的面积为20平方米,求图中四个小三角形的面积和,即S1+S2+S3+S4=
 查看习题详情和答案>>
查看习题详情和答案>>

