摘要： 如右图所示.已知点C的坐标是(2,2).过点C的直线CA与x轴交于点A.过点C且与直线CA垂直的直线CB与y轴交于点B.设点M是线段AB的中点.求点M的轨迹方程． 解法一::设M的坐标为(x.y)． 若直线CA与x轴垂直.则可得到M的坐标为(1,1)． 若直线CA不与x轴垂直.设直线CA的斜率为k.则直线CB的斜率为-.故直线CA方程为:y＝k(x-2)+2. 令y＝0得x＝2-.则A点坐标为． CB的方程为:y＝-(x-2)+2.令x＝0.得y＝2+. 则B点坐标为.由中点坐标公式得M点的坐标为① 消去参数k得到x+y-2＝0(x≠1). 点M(1,1)在直线x+y-2＝0上. 综上所述.所求轨迹方程为x+y-2＝0. 解法二:设M(x.y).依题意A点坐标为(2x,0).B点坐标为(0,2y)． ∵|MA|＝|MC|. ∴＝. 化简得x+y-2＝0. 解法三:依题意|MA|＝|MC|＝|MO|. 即:|MC|＝|MO|.所以动点M是线段OC的中垂线.故由点斜式方程得到:x+y-2＝0.
网址：http://m.1010jiajiao.com/timu_id_4007104[举报]
如图所示，已知椭圆M：| y2 |
| a2 |
| x2 |
| b2 |
| 12 |
| 5 |
（1）求椭圆M的方程；
（2）试判断直线l与x轴是否交于定点？若是，求出定点的坐标；若不是，请说明理由．
如图所示，F1、F2分别为椭圆C：| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| 2 |
（1）求椭圆C的方程和焦点坐标；
（2）设点M是椭圆上的动点N（0，
| 1 |
| 2 |
（3）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
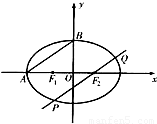
如图所示，F1、F2分别为椭圆C：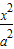
+
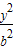=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，
）到F1、F2两点的距离之和为4．
（1）求椭圆C的方程和焦点坐标；
（2）设点M是椭圆上的动点N（0，
），求|MN|的最大值．
（3）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
查看习题详情和答案>>
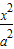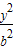+=1（a＞b＞0）的左、右两个焦点，A、B为两个顶点，已知椭圆C上的点（1，）到F1、F2两点的距离之和为4．（1）求椭圆C的方程和焦点坐标；
（2）设点M是椭圆上的动点N（0，
），求|MN|的最大值．（3）过椭圆C的焦点F2作AB的平行线交椭圆于P、Q两点，求△F1PQ的面积．
查看习题详情和答案>>
(2007
北京崇文模拟)如图所示，已知双曲线C的中心点为坐标原点O，焦点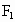
、
在x轴上，点P在双曲线的左支上，点M在右准线上，且满足
，
．
(1)
求双曲线C的离心率e；(2)
若双曲线C过点Q(2，
)，
、
是双曲线虚轴的上、下端点，点A、B是双曲线上不同的两点，且
，
，求直线AB的方程．
下图展示了一个由区间
（其中
为一正实数)到实数集R上的映射过程：区间中的实数
对应线段
上的点
，如图1；将线段围成一个离心率为
的椭圆，使两端点
、
恰好重合于椭圆的一个短轴端点，如图2 ；再将这个椭圆放在平面直角坐标系中，使其中心在坐标原点，长轴在
轴上，已知此时点的坐标为
，如图3，在图形变化过程中，图1中线段
的长度对应于图3中的椭圆弧ADM的长度.图3中直线与直线
交于点
，则与实数对应的实数就是
，记作
,
现给出下列5个命题
①
；
②函数
是奇函数；③函数在
上单调递增； ④.函数的图象关于点
对称；⑤函数
时AM过椭圆的右焦点.其中所有的真命题是: （ ）
A.①③⑤ B.②③④ C.②③⑤ D.③④⑤
查看习题详情和答案>>