摘要:处理方法:引入辅助角 .化为y=sin(x+),利用函数即可求解.Y=asinx+bsinxcosx+mcosx+n型亦可以化为此类. 例3 .已知f(x)=2cosx+sin2x+a,若x<2,求a的取值范围. 注:本题综合运用三角恒等变形.三角函数的单调性.不等式的性质.函数的恒成立等知识.是一个较好的三角函数综合题. 例4.求函数y=a sin x + b cos x的最值. 解:y=a sin x + b cos x=sin(x + arc tg) ∴当x=2k+--arc tg时.ymax = 当x=2k+--arc tg时.ymin =-- 例5.求函数y= sin2x+2sinx cosx+3 cos2x的最小值.最大值.并写出函数y 取 最值时的x的集合. 解:∵y= sin 2x + 2cos2x + 1 = sin 2x + cos 2x + 2 = sin(2x +)+ 2 ∴当sin(2x +)= --1时. 有ymin = 2 --. 当sin(2x +)= 1时.有ymax = 2 +. 此时有2x + = 2k--, x = k-- (kz) 2x + = 2k + , x = k+ (kz) 故函数y取最小值2--时x 的集合是{x∣x = k--, kz } y取最大值2 +时x 的集合是{x∣x = k+, kz } 从上面三例可以清晰地看出.这一类的三角函数的最值求解中运用的基本的方法是“利用辅助角法 .将较复杂的三角式转化成“Asin() 的形式.将异名三角比化归成同名三角比.同时.也应对自变量的取值范围要仔细地考察.
网址:http://m.1010jiajiao.com/timu_id_4005975[举报]
阅读下面材料:根据两角和与差的正弦公式,有
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
,β=
代入③得 sinA+subB=2sin
cos
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=β 有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+subB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)求值:sin220°+cos250°+sin20°cos50°(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
(2012•福建模拟)阅读下面材料:
根据两角和与差的正弦公式,有sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=B有α=
,β=
代入③得 sinA+sinB=2sin
cos
.
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
sin
;
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=2sin2C,试判断△ABC的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
查看习题详情和答案>>
根据两角和与差的正弦公式,有sin(α+β)=sinαcosβ+cosαsinβ------①
sin(α-β)=sinαcosβ-cosαsinβ------②
由①+②得sin(α+β)+sin(α-β)=2sinαcosβ------③
令α+β=A,α-β=B有α=
| A+B |
| 2 |
| A-B |
| 2 |
代入③得 sinA+sinB=2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅰ)类比上述推证方法,根据两角和与差的余弦公式,证明:cosA-cosB=-2sin
| A+B |
| 2 |
| A-B |
| 2 |
(Ⅱ)若△ABC的三个内角A,B,C满足cos2A-cos2B=2sin2C,试判断△ABC的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
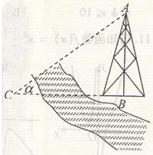 如图,测量河对岸的塔形建筑AB,A为塔的顶端,B为塔的底端,河两岸的地面上任意一点与塔底端B处在同一海拔水平面上,现给你一架测角仪(可以测量仰角、俯角和视角),再给你一把尺子(可以测量地面上两点问距离),图中给出的是在一侧河岸地面C点测得仰角∠ACB=α,请设计一种测量塔形建筑高度AB的方法(其中测角仪支架高度忽略不计,计算结果可用测量数据所设字母表示).
如图,测量河对岸的塔形建筑AB,A为塔的顶端,B为塔的底端,河两岸的地面上任意一点与塔底端B处在同一海拔水平面上,现给你一架测角仪(可以测量仰角、俯角和视角),再给你一把尺子(可以测量地面上两点问距离),图中给出的是在一侧河岸地面C点测得仰角∠ACB=α,请设计一种测量塔形建筑高度AB的方法(其中测角仪支架高度忽略不计,计算结果可用测量数据所设字母表示).