题目内容
由“若直角三角形两直角边的长分别为a,b,将其补成一个矩形,则根据矩形的对角线长可求得该直角三角形外接圆的半径为r=
| ||
| 2 |
分析:直角三角形对应三棱锥三条侧棱两两垂直,直角三角形补成一个矩形可类比空间三棱锥补一个长方体,而球的内接长方体的体对角线就是球的直径.
解答:解:若三棱锥三条侧棱两两垂直,
侧棱长分别为a,b,c,
可补成一个长方体,体对角线长为
,
而体对角线就是外接球的直径,
故答案为
.
侧棱长分别为a,b,c,
可补成一个长方体,体对角线长为
| a2+b2+c2 |
而体对角线就是外接球的直径,
故答案为
| ||
| 2 |
点评:本题考查了类比推理,由平面性质类比空间性质

练习册系列答案
相关题目
 ,面积为S,则其内切圆半径
,面积为S,则其内切圆半径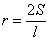 ”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径
”类比可得“若三棱锥表面积为S,体积为V,则其内切球半径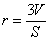 ”;乙:由“若直角三角形两直角边长分别为
”;乙:由“若直角三角形两直角边长分别为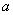 ,b,则其外接圆半径
,b,则其外接圆半径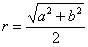 ”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为
”;类比可得“若三棱锥三条侧棱两两垂直,侧棱长分别为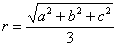 ”.这两位同学类比得出的结论 ( )
”.这两位同学类比得出的结论 ( )