题目内容
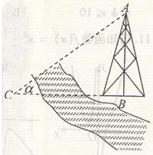如图，测量河对岸的塔形建筑AB，A为塔的顶端，B为塔的底端，河两岸的地面上任意一点与塔底端B处在同一海拔水平面上，现给你一架测角仪（可以测量仰角、俯角和视角），再给你一把尺子（可以测量地面上两点问距离），图中给出的是在一侧河岸地面C点测得仰角∠ACB=α，请设计一种测量塔形建筑高度AB的方法（其中测角仪支架高度忽略不计，计算结果可用测量数据所设字母表示）．
分析：河的这岸选取一点D，测得CD=6，并测得∠BCD=γ，∠BDC=β，进而求得∠CBD，利用正弦定理求得BC，进而在Rt△ABC中，根据AB=BCtan∠ACB求得答案．
解答：
解：在河的这岸选取一点D，测得CD=6，并测得∠BCD=γ，∠BDC=β，
在△BCD中，∠CBD=π-γ-β
由正弦定理得
=
∴BC=
在Rt△ABC中，AB=BCtan∠ACB=
解：在河的这岸选取一点D，测得CD=6，并测得∠BCD=γ，∠BDC=β，在△BCD中，∠CBD=π-γ-β
由正弦定理得
| BC |
| sin∠BDC |
| CD |
| sin∠CBD |
∴BC=
| bsinβ |
| sin(β+γ) |
在Rt△ABC中，AB=BCtan∠ACB=
| bsinβtanα |
| sin(β+γ) |
点评：本题主要考查了解三角形的实际应用．考查了学生运用所学知识解决实际问题的能力．
练习册系列答案
阅读快车系列答案
相关题目
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=75°，∠BDC=60°，CD=60米，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个侧点C与D．现测得∠BCD=α，∠BDC=β，CD=s，并在点C测得塔顶A的仰角为θ，则塔高AB=
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D，现测得∠BCD=45°，∠BDC=60°，CD=10m，并在点C测得塔顶A的仰角为45°，则塔高AB=
如图，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD=15°，∠BDC=30°，CD=30，并在点C测得塔顶A的仰角为60°，则塔高AB=（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个测点C与D．测得∠BDC=30°，CD=30米，并在点C测得塔顶A的仰角为60°，