摘要： 不等式大小比较的常用方法:(1)作差:作差后通过分解因式.配方等手段判断差的符号得出结果,(2)作商(常用于分数指数幂的代数式),平方法,有理化,(6)利用函数的单调性,(7)寻找中间量或放缩法 ,(8)图象法.其中比较法是最基本的方法.如(1)设.比较的大小(答:当时.(时取等号),当时.(时取等号)),(2)设...试比较的大小(答:),(3)比较1+与的大小(答:当或时.1+＞,当时.1+＜,当时.1+＝)
网址：http://m.1010jiajiao.com/timu_id_4004497[举报]
根据定义讨论(或证明)函数增减性的一般步骤是：
(1)设x1、x2是给定区间内的任意两个值且x1＜x2；
(2)作差f(x1)－f(x2)，并将此差化简、变形；
(3)判断f(x1)－f(x2)的正负，从而证得函数的增减性．
利用函数的单调性可以把函数值的大小比较的问题转化为自变量的大小比较的问题．
函数的单调性只能在函数的定义域内来讨论．这即是说，函数的单调区间是其定义域的________．
如果执行右边的程序框图，输入正整数N(N≥2)和实数a1,a2,…,aN，输出A,B，则
（A）A+B为a1,a2,…,aN的和
（B）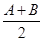
为a1,a2,…,aN的算术平均数
（C）A和B分别是a1,a2,…,aN中最大的数和最小的数
（D）A和B分别是a1,a2,…,aN中最小的数和最大的数
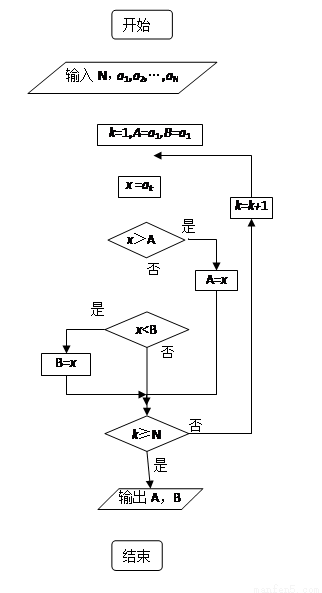
【解析】根据程序框图可知，这是一个数据大小比较的程序，其中A为最大值，B为最小值，选C.
查看习题详情和答案>>
已知等差数列{an}满足：a1+a2n-1=2n，n∈N*，设Sn是数列{
}的前n项和，记f（n）=S2n-Sn．
（1）求an；
（2）比较f（n+1）与f（n）的大小；
（3）（理）若不等式log2t+log2x+log2（2-x）-log2（12f（n））-3＜0对一切大于1的自然数n和所有使不等式有意义的实数x都成立，求实数t的取值范围．
（文）如果函数g（x）=x2-3x-3-12f（n）对于一切大于1的自然数n，其函数值都小于零，求x的取值范围．
查看习题详情和答案>>
| 1 | an |
（1）求an；
（2）比较f（n+1）与f（n）的大小；
（3）（理）若不等式log2t+log2x+log2（2-x）-log2（12f（n））-3＜0对一切大于1的自然数n和所有使不等式有意义的实数x都成立，求实数t的取值范围．
（文）如果函数g（x）=x2-3x-3-12f（n）对于一切大于1的自然数n，其函数值都小于零，求x的取值范围．