摘要：9．解不等式: 解:原不等式 ①∴a=2时,不等式的角为x>; ②a>2时,a-2>0, 故原不等式解为<x≤0或x≥a-2 ③当1<a<2时.a-2<0. ∴原不等式解为<x≤a-2或x≥0
网址：http://m.1010jiajiao.com/timu_id_4004426[举报]
古希腊数学家丢番图（公元250年前后）在《算术》中就提到了一元二次
方程的问题，不过当时古希腊人还没有寻求到它的求根公式，只能用图解等方法来求解。在欧几里得的《几何原本》中，形如
（a>0,b>0）的方程的图解法是：如图，以
和b为两直角边做Rt△ABC,再在斜边上截取
，则AD的长就是所求方程的解。
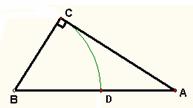
（1）请用含字母a、b的代数式表示AD的长。
（2）请利用你已学的知识说明该图解法的正确性，并说说这种解法的遗憾之处。
查看习题详情和答案>>
选考题请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若g(x)=
| 1 | ||
|
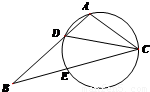
22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆C：
|
| π |
| 3 |
（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
选考题
请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若
定义域为R，求实数m的取值范围．
22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆
上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与半圆C上的弧AP的长度均为
（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
查看习题详情和答案>>
请从下列三道题当中任选一题作答，如果多做，则按所做的第一题计分，请在答题卷上注明题号．
22-1设函数f（x）=|2x-1|+|2x-3|
（1）解不等式f（x）≤5x+1；
（2）若
定义域为R，求实数m的取值范围．22-2如图，在△ABC中，CD是∠ACB的角平分线，△ACD的外接圆交BC于E，AB=2AC，
（1）求证：BE=2AD；
（2）当AC=1，BC=2时，求AD的长．
22-3已知P为半圆
上的点，点A的坐标为（1，0），O为坐标原点，点M在射线OP上，线段OM与半圆C上的弧AP的长度均为（1）求以O为极点，x轴的正半轴为极轴建立极坐标系，求点M的极坐标；
（2）求直线AM的参数方程．
查看习题详情和答案>>
已知二次函数y＝f1(x)的图象以原点为顶点且过点(1，1)，反比例函数y＝f2(x)的图象与直线y＝x的两个交点间的距离为8，f(x)＝f1(x)＋f2(x)
(1)求函数f(x)的表达式；
(2)求证：当a＞3时，关于x的方程f(x)＝f(a)有三个不相等的实数解
| |||||||||||||||