摘要： 利用反证法 例12 已知函数f上是增函数,a,b∈R,若f.求证:a+b≥0. 证明 假设a+b<0,则a<-b,b<-a, ∵ 函数f上是增函数, ∴ f <f(-a), ∴ f+f(-b),这与已知矛盾, ∴ a+b<0不成立,即a+b≥0. 例13 设函数f(x)对定义域内任意实数都有ff(y)成立,求证:对定义域内任意x,都有f(x) >0. 证明 假设在定义域内存在x0,使f(x0)≤ 0, ∵ ∴ f(x0) >0,这与假设的f(x0)≤ 0矛盾, 所以假设不成立,故对定义域内任意x,都有f(x) >0. 以上我们利用抽象函数的特殊模型.函数性质.特殊方法等途径举例说明了求解抽象函数问题的一些策略.事实上处理这类问题时,常将几种解题策略综合使用,“多管齐下 方能游刃有余.
网址：http://m.1010jiajiao.com/timu_id_4003200[举报]
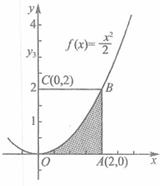如图，利用随机模拟的方法可以估计图中由曲线y=| x2 |
| 2 |
①先产生两组0～1的均匀随机数，a=rand （ ），b=rand （ ）；
②做变换，令x=2a，y=2b；（3）产生N个点（x，y），并统计满足条件y＜
| x2 |
| 2 |
为了检验某套眼睛保健操预防学生近视的作用，把500名做过该保健操的学生与另外500名未做该保健操的学生视力情况记录作比较，提出假设H0：“这套眼睛保健操不能起到预防近视的作用”，利用2×2列联表计算的K2≈3.918．经查对临界值表知P（K2≥3.841）=0.05．对此，四名同学做出了以下的判断：
P：有95%的把握认为“这种眼睛保健操能起到预防近视的作用”；
q．若某人未做眼睛保健操，那么他有95%的可能性得近视；
r：这种眼睛保健操预防近视的有效率为95%；
s：这种眼睛保健操预防近视的有效率为5%，
则下列结论中，正确结论的序号是（ ）
①p∧?q； ②?p∧q； ③（?p∧?q）∧（r∨s）； ④（p∨?r）∧（?q∨s）．
P：有95%的把握认为“这种眼睛保健操能起到预防近视的作用”；
q．若某人未做眼睛保健操，那么他有95%的可能性得近视；
r：这种眼睛保健操预防近视的有效率为95%；
s：这种眼睛保健操预防近视的有效率为5%，
则下列结论中，正确结论的序号是（ ）
①p∧?q； ②?p∧q； ③（?p∧?q）∧（r∨s）； ④（p∨?r）∧（?q∨s）．
| A、①③ | B、②④ | C、①④ | D、都不对 |